Demystifying bitwise operations, a gentle C tutorial

This tutorial is in early draft. If you see any errors, feedback is greatly appreciated.

Bitwise operations are a fundamental part of Computer Science. They help Software Engineers to have a deeper understanding of how computers represent and manipulate data, and they are crucial when writing performance-critical code. Truth being said, nowadays, they are rarely used in the business code we write, and they stay hidden in libraries, frameworks, or low-level system programming codebases. The reason is simple: writing code that operates on bits can be tedious, less readable, not always portable, and, most importantly, error-prone. Modern programming languages nowadays have higher-level abstractions that replace the need for bitwise operations and “constructs”, and trading (potential) small performance and memory gains for readability is not such a bad deal. Plus, compilers are more intelligent nowadays and can optimise your code in ways you (and I) cannot even imagine.

To better understand my arguments, not so long ago, I’ve written a snake in C that uses only bitwise operations and squeezes everything into only a handful of uint32_t and uint64_t variables. The results (after macro expansions) are not that readable, even for an initiated eye.

In any case, this article is not about why we shouldn’t ever touch them; on the contrary, it is about why they are cool and how they can make specific code snippets orders of magnitude faster than the “higher-level-readable-modern approach”. If you are a programmer who enjoys competitive programming, knowing bitwise operations (in case you don’t know about them already) will help you write more efficient code.

Again, knowing how to deal with bitwise operations is necessary if you plan a career in systems programming, network programming or embedded software development.

Table of contents

• Table of contents
• Number systems
• A certain symmetry and patterns
• Numbers and Data Types in C
• Transforming numbers from the decimal to other number systems (binary, hexadecimal, etc.)
• Bitwise operations
  • Bitwise AND
  • Bitwise OR
  • Bitwise XOR
  • Bitwise NOT
  • Left Shift
  • Right Shift
• Negative numbers and their binary representation
• Pitfalls to avoid when using bitwise operations
• Mandatory Computer Science Exercise - The solitary integer
• Printing numbers in binary by using bitwise operations
• Masking
• The power of masking - Pairwise Swap
• Getting, Setting, Clearing, Toggling the nth bit
  • Getting the nth bit of a number
  • Setting up the nth bit of a number
  • Toggling the nth bit of a number
• Getting, Setting, Clearing, and Toggling a bit portion of a number
  • Clearing the last bits of a number
  • Replacing multiple bits
  • Reading multiple bits
• Bitwise operations and their relationship with the powers of two
  • Multiplying a number with a power of two
  • Dividing a number with a power of two
  • Checking if a number is even or odd
  • Getting the remainder when we divide with a power of two
  • Determining if an integer is a power of two
  • Getting the next power of two
• Implementing a BitSet (or BitVector)
  • SET_NW
  • SET_W
  • SET_MASK
  • SET_DECLARE
  • SET_1 and SET_0
  • SET_GET
  • Using the BitSet
• Swapping two numbers
• Bitwise operations and chars
• Gray codes and permutations
• That’s it
• References

Number systems

Nature gifted humankind ten fingers. As a direct consequence of Nature’s decision, our Math (and numbers) are almost always expressed in base 10. If an alien specie (with eight fingers) discovers mathematics, they will probably use base 8 (octal) to represent their numbers. Meanwhile, computers love base 2 (binary) because computers have only two fingers: 1 and 0, or one and none.

The Mayan numeral system was the system to represent numbers and calendar dates in the Maya civilization. It was a vigesimal (base-20) positional numeral system.

In mathematics, a base refers to the number of distinct symbols we use to represent and store numbers.

In our case (decimal), those symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. We must “recombine” the existing symbols to express more significant numbers. For example, 127 is defined by re-using 1, 2, and 7. The three symbols are combined to express a greater quantity that cannot be described using mere fingers.

By far, the most popular number system bases are:

Number System	Base	Symbols
Binary	2	[0, 1]
Octal	8	[0, 1, 2, 3, 4, 5, 6, 7 ]
Decimal	10	[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Hexadecimal	16	[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F]

To make things more generic, if \(b\) is the base, to write the number natural number \(a\) in base \(b\) (notation is \(a_{b}\)), then the formula is: \(a_{b}=a_{0}*b^{0}+a_{1}*b^{1}+a_{2}*b^{2}+...+a_{n}*b^{n}\), where \(a_{n}\), \(a_{n-1}\), …, \(a_{2}\), \(a_{1}\), \(a_{0}\) are the symbols in descending order, and \(a_{i} \lt b\).

For example, 1078 in base 10 (\(b=10\), so \(a_{i} \in \{0,1,2,3,4,5,6,7,8,9\}\)) can be written as:

\[1078_{10} = 1 * 10^3 + 0 * 10^2 + 7 * 10^1 + 8 * 10^0\]

If we were to change the base and write 1078 from base 10 to base 7, then \(b=7\) and \(a_{i} \in \{0,1,2,3,4,5,6\}\) (we only have seven fingers numerotated from 0 to 6):

\[1078_{10} = 3 * 7^3 + 1 * 7^2 + 0 * 7^1 + 0 * 7^0 = 3100_{7}\]

If we are to change the base and write 1078 from base 10 to base 2, then \(b=2\) and \(a_{i} \in \{0,1\}\):

\[1078_{10} = \\ 1 * 2^{10} + 0 * 2^9 + 0 * 2^8 + 0 * 2^7 + 0 * 2^6 + \\ 1 * 2^5 + 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0 \\ = 10000110110_{2}\]

As we’ve said earlier, computer store numbers in binary, so better visualise how our memory looks like, let’s take a look at the following diagram:

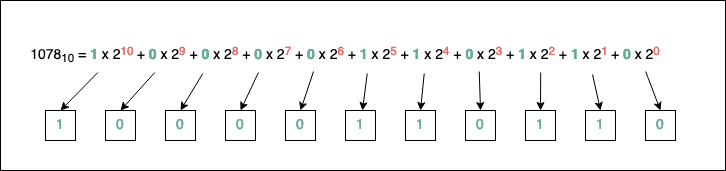
As you can see, to identify the bits (the sequence of zeroes and ones which are the acceptable symbols in binary) comprising the number, we have to find an algorithm to determine the numbers \(a_{i}\). Luckily, such an algorithm exists, and it’s straightforward to implement. It works the same, no matter what base we pick.

Based on the above picture, another important observation is that to represent the number 1078 in binary, we need at least ten memory cells (bits) for it (look at the most significant power of 2 used, which is 10). As a side rule, the fewer symbols we have for our base, the more we have to repeat existing symbols. If we want to go extreme and pick b=1, we will have a Unary Numeral System, where representing a number N is equivalent to repeating the unique symbol of the system N times.

The algorithm for transitioning a number to any base \(b\) is as follows:

1. We convert the number to the decimal base;
2. We divide the decimal representation of the number by the base \(b\);
3. We record the reminder to the division (this will be a digit in the base \(b\) representation);
4. We continue dividing the quotient with base \(b\) and keep recording the remainder;
5. If the quotient becomes 0 at some point, we stop.

The base \(b\) representation of the decimal number will be the sequence of remainders (in reverse order).

For example, let’s convert 35 to base 2:

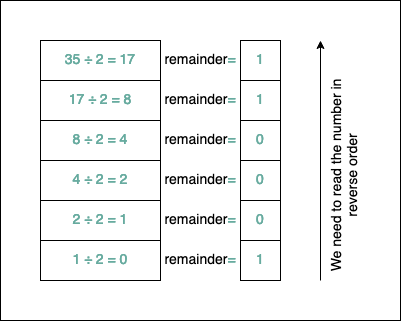
After applying the algorithm, \(35_{10}=100011_{2}\). It’s easy to test if things are correct. We take each bit and multiply its corresponding power of b=2: \(35_{10}=1*2^{5}+0*2^{4}+0*2^{3}+0*2^{2}+1*2^{1}+1*2^{0}\).

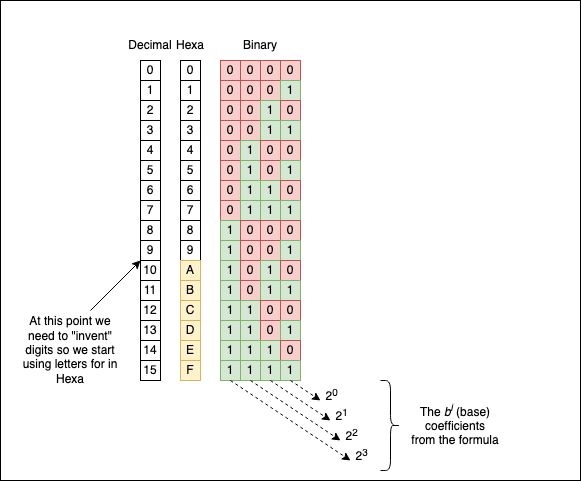
Converting a number from the decimal system to the hexadecimal number system is a little bit trickier; the algorithm remains the same, but because the hexadecimal system has 16 symbols, and we only have ten digits (0, 1,…, 9) we need to add additional characters to our set, the letters from A to F. A corresponds to 10, B corresponds to 11, C corresponds to 12, D corresponds to 13, E corresponds to 14, and F corresponds to 15.

For example, let’s convert 439784 to hexadecimal to see how it looks:

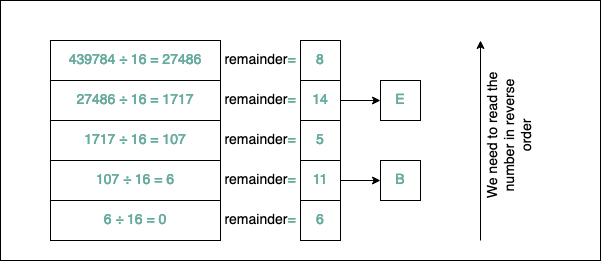
As you can see, \(439784_{10}=6B5E8_{16}\). Another popular notation for hexadecimal numbers is 0x6B5E8; you will see the 0x prefix before the number. Similarly, for binary, there’s the 0b prefix before the actual number representation (C doesn’t support this).

Because numbers in the binary numerical system take so much “space” to be represented, you will rarely see them printed in binary, but you will see them in hexadecimal.

Personally, when I have to “translate” from binary to hexadecimal, and vice-versa, I don’t apply any “mathematical” algorithm. There’s a simple “visual” correspondence we can use:

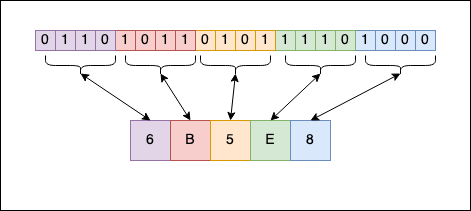
As you can see, each symbol from the hexadecimal format can be represented as a sequence of 4 bits in binary. 8 is 1000, E is 1110, and so on… When you concatenate everything, you have the binary representation of the number from hexadecimal to binary. The reverse operation also works. With a little bit of experience (no pun intended), you can do the “transformation” in your head and become one of the guys from The Matrix.

If you don’t have experience with the hexadecimal number systems, write the digits on a piece of paper a few times until you memorise them:

A certain symmetry and patterns

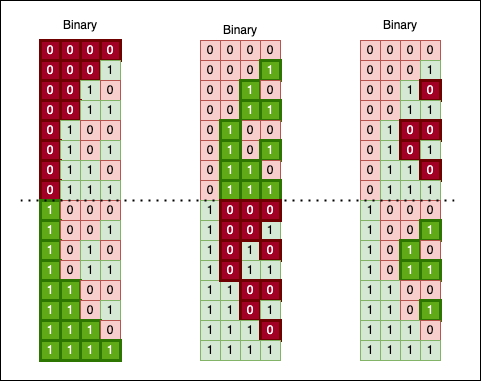
Numbers, especially when represented in binary, have a certain symmetry associated with them. The most obvious pattern is the way odd and even numbers have to alternate 0 and 1 as their last (least significant) bit:

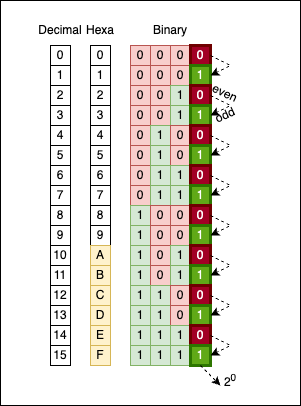
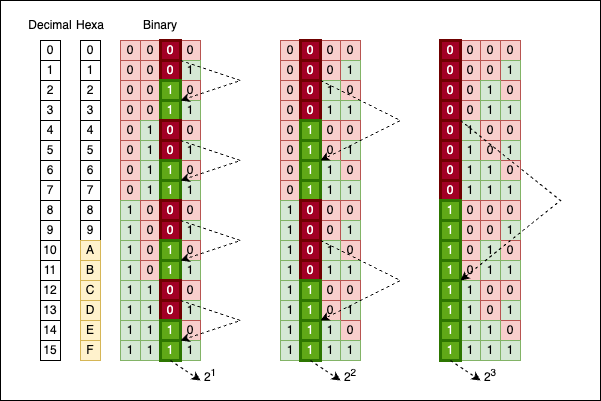
There’s no magic; this is the way numbers operate. If we move one column to the left (the bits corresponding to \(2^1\)), you will see every two (\(2^1\)) bits alternating: 00 alternates with 11.

If we move one more column to the left (to the bits corresponding to \(2^2\)), you will see every four bits (\(2^2\)) alternating: 0000 alternates with 1111.

If we move just another column to the left (to the bits corresponding to \(2^3\)), you will see every eight bits (\(2^3\)) alternating: 00000000 alternates with 11111111.

Another interesting way to look at the numbers in binary is to “cut” their representation in half and observe a “mirroring” effect:

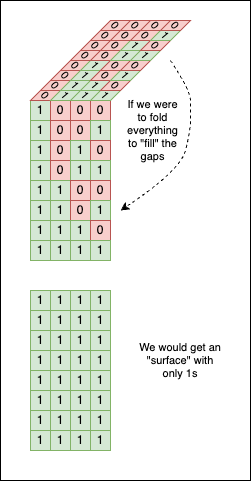
If we were to use our imagination, we could even fold the “bit surface”; we would get only a “surface” of 1 bits, as the upper chunk will fill up the gaps in the lower one:

Another interesting pattern is looking at a “ladder” forming up, where each step is double the size of the previous one (look at the green line from the image below):

“The ladder” changes its step whenever it encounters a power of two. Also, if you look closer, every power of two has only one bit of 1 at the power’s position in the number.

Numbers and Data Types in C

The C programming language provides numeric data types to store numbers in the computer’s memory. As previously mentioned, they are stored in binary (as a sequence of zeroes and ones). I am sure you’ve heard about char, int, unsigned int, long, long long, float, etc. If you want to revamp your knowledge in this area, I guess this Wikipedia article is more than enough. The biggest problem with the “classic” types was that their size could differ from one machine to another.

For example, char is defined in the standard as an integer type (that can be signed or unsigned) that contains CHAR_BIT bits of information. On most machines, CHAR_BIT is 8, but there were machines where for reasons beyond the scope of this article, CHAR_BIT was 7. Working on the bits of a char and assuming they are 8 (99.99% of the cases) would create portability problems on the much fewer systems where CHAR_BIT is 7. (Note: CHAR_BIT is a macro defined in limits.h)

The same goes for the typical int. In the C standard, int doesn’t have a fixed size in terms of the bits it contains, only a lower bound, meaning it should be a least 16 bits long; on my machine is 32, so again, portability issues are in sight.

With C99, new fixed-length data types were introduced to increase the portability of the software we write. They can be found in the header file inttypes.h (and in stdint.h). Those are the types I prefer to use nowadays when I write C code:

• int8_t : signed integer with 8 bits;
• int16_t : signed integer with 16 bits;
• int32_t : signed integer with 32 bits;
• int64_t : signed integer with 64 bits;

For each intN_t signed integer, there is also an uintN_t counterpart (unsigned integer, N=8,16,32,64). For this reason, we will use the fixed-size integers from stdint.h in our code.

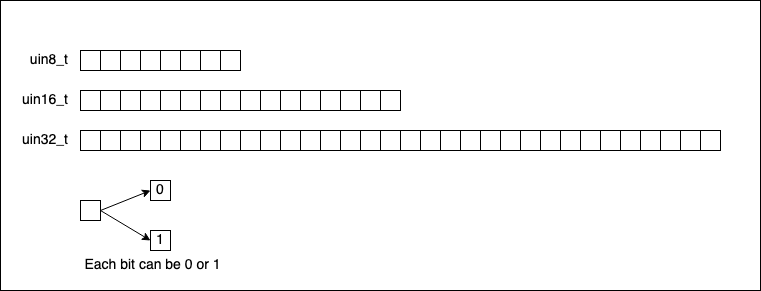
Letting signed integers aside for a moment (as we will discuss later how negative numbers are represented), if we were to visually represent uint8_t, uint16_t and uint32_t (skipping uint64_t), they look like this:

The maximum value an uint8_t variable can take is when all its bits are set to 1:

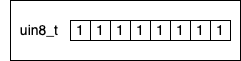
To determine the maximum unsigned integer we can hold in a variable of type uint8_t, we add all the powers of two like this:

\[m = 1 * 2^7 + 1 * 2^6 + 1 * 2^5 + 1 * 2^4 + 1 * 2^3 + 1 * 2^2 + 1 * 2^1 + 1 * 2^0 = \\ = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = \\ = 255\]

Or, we can use this formula: \(\sum_{i=0}^{n} 2^i =2^{n+1}-1\), so for each uintN_t we can up with this table:

Unsigned Fixed Type	Maximum Value	C Macro
uint8_t	28-1=255	UINT8_MAX
uint16_t	216-1=65535	UINT16_MAX
uint32_t	232-1=4294967295	UINT32_MAX
uint64_t	264-1=18446744073709551615	UINT64_MAX

Yes, you’ve read well; there are also macros for all the maximum values. When you are programming, you don’t have to compute anything; it will be a waste of CPU time to redo the math all over again. So everything is stored as macro constants (if such a thing exists):

#include <stdio.h>
#include <stdint.h> // macros are included here

int main(void) {
    printf("%hhu\n", UINT8_MAX);
    printf("%hu\n", UINT16_MAX);
    printf("%u\n", UINT32_MAX);
    printf("%llu\n", UINT64_MAX);
    return 0;
}

Output:

255
65535
4294967295
18446744073709551615

In the code section, there’s one slight incovenience, %hhu, %hu, %u, etc. are not the right formats for the fixed-length types. To the right fornats are defined in inttypes.h as macros:

#include <stdio.h>
#include <stdint.h> // macros are included here

int main(void) {
    printf("%+"PRIu8"\n", UINT8_MAX);
    printf("%+"PRIu16"\n", UINT16_MAX);
    printf("%+"PRIu32"\n", UINT32_MAX);
    printf("%+"PRIu64"\n", UINT64_MAX);
    return 0;
}

Funnily enough on clang I get warnings for using those formats, while on gcc everything compiles just fine, without any warnings:

bits.c:300:26: warning: format specifies type 'unsigned char' but the argument has type 'int' [-Wformat]
    printf("%"PRIu8"\n", UINT8_MAX);
            ~~~~~~~      ^~~~~~~~~
/Library/Developer/CommandLineTools/SDKs/MacOSX.sdk/usr/include/stdint.h:107:27: note: expanded from macro 'UINT8_MAX'
#define UINT8_MAX         255
                          ^~~
bits.c:301:27: warning: format specifies type 'unsigned short' but the argument has type 'int' [-Wformat]
    printf("%"PRIu16"\n", UINT16_MAX);
            ~~~~~~~~      ^~~~~~~~~~
/Library/Developer/CommandLineTools/SDKs/MacOSX.sdk/usr/include/stdint.h:108:27: note: expanded from macro 'UINT16_MAX'
#define UINT16_MAX        65535

Transforming numbers from the decimal to other number systems (binary, hexadecimal, etc.)

For this exercise, we will write a C function that takes an uint16_t and prints its representation in other numerical systems to stdout.

For everything bigger than base 10, we will use the letters from the alphabet. If the base is bigger than 36 (10 digits + 26 letters), we will print an error to the stderr. We will start by defining an “alphabet” of symbols that map every number from 0..35 to the digits and letters that we have available:

#define MAX_BASE 36
char symbols[MAX_BASE] = {
    '0', '1', '2', '3', '4', '5', '6', '7', '8',
    '9', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H',
    'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q',
    'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z'
};
// For 0, symbols[0] = '0'
// ...
// For 11, symbol[11] = 'B'
// ...
// For 35, symbol[35] = 'Z'

The next step is to write a function that implements the basic algorithm described in the first section of the article.

#define MAX_BASE 36
char symbols[MAX_BASE] = { /** numbers and letters here */ };
void print_base_iter1(uint16_t n, uint8_t base) {
    // Sanity check
    if (base >= MAX_BASE){
        fprintf(stderr, "Base %d is bigger than the possible accepted base", base);
        return;
    }
    uint16_t r;
    while (n>0) { // While quotient is bigger than 0
        r = n % base; // Compute the remainder
        n /= base; // Divide with base again
        fprintf(stdout, "%c", symbols[r]); // Print the symbol
                                           // Associated with the remainder
    }
}

Everything looks good, but if we run the function, we will see a slight inconvenience; the symbols are printed in the reverse order we want them to be. For example, calling: print_base_iter1(1078, 2); will yield the result: 01101100001, which is technically correct, but only if we read the number from right to left or use a mirror. Jokes aside, the correct answer is 10000110110.

Now let’s try to convert a number from decimal to hexadecimal to see some letters by printing print_base_iter1(44008, 16);, the result given by our function is 8EBA, again if we read it from right to left, it’s “the excellent” result.

To fix this inconvenience, we can write the results in an intermediary, char* (string), to control the order in which we show the characters. Or we can use a Stack data structure, where we push the remainders individually and then print them while we pop them out.

Another simpler solution is to use recursion + the only stack real programmers use (that was a joke!):

#define MAX_BASE 36
char symbols[MAX_BASE] = { /** */ };
static void print_base_rec0(uint16_t n, uint8_t base, uint16_t rem) {
    if (n>0) {
        uint16_t r=n%base;
        print_base_rec0(n/base, base, r); // calls the method again
                                          // printing the character from the next line
                                          // doesn't happen until the previous call to 
                                          // the method is finished
        fprintf(stdout, "%c",symbols[r]);
    }
}
void print_base_rec(uint16_t n, uint8_t base) {
    if (base>=MAX_BASE) {
        fprintf(stderr, "Base %d is bigger than the possible accepted base", base);
        return; 
    }
    print_base_rec0(n, base, 0);
}

To simplify things, C supports hexadecimal literals (but not binary!), so we can assign numbers in hexadecimal to variables. In C, a hexadecimal literal is written with the prefix 0x (or 0X) followed by one or more hexadecimal symbols (digits). Both uppercase and lowercase work.

For example, we can write:

uint32_t x = 0x3Fu;    // 0x3F is 63  
                       // another way of writing: 
                       //
                       //            uint32_t x = 63

uint32_t y = 0xABCDu;  // 0xABCD is 43981
                       // another way of writing: 
                       //            
                       //            uint32_t x = 43981

We can also print the hexadecimal representation of a number using "%X" (uppercase letters) or "%x" (lowercase letters) as the format specifier:

int main(void) {
    printf("%x\n", 63);
    printf("%X\n", 43981);
    return 0;
}

// Output;
// 3f
// ABCD

Hexadecimal literals allow us to insert easter eggs in our code base. For example, this simple line can act as a warning for developers just about to join your project:

printf("%x %x %x %x\n", 64206, 10, 2989, 49374);

// Output:
// face a bad c0de  

Unfortunately, in C, there’s no binary literal…

Bitwise operations

Bitwise operations are mathematical operations that manipulate the individual bits of a number (or set of numbers). As the name suggests, they work on bits.

The operations are:

Symbol	Operation
&	bitwise AND
|	bitwise OR
^	bitwise XOR
~	bitiwse NOT

Additionally, you have two more operations to shift bits (right or left) inside a number.

Symbols	Operation
<<	left SHIFT
>>	right SHIFT

If we apply one of the binary operators on two numbers, A and B, we obtain a third number , C, where C = A OP B.

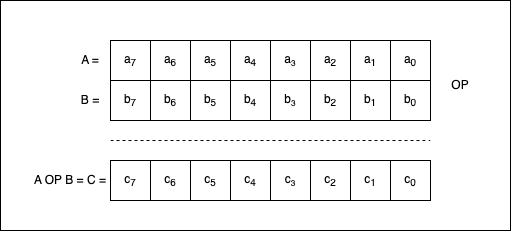
If \(a_{7}, a_{6}, ..., a_{0}\) are the bits composing A, \(b_{7}, b_{6}, ..., b_{0}\) are the bits composing B, and \(c_{7}, c_{6}, ..., c_{0}\) are bits composing C, then we can say that:

• \(c_{7} = a_{7} \text{ OP } b_{7}\);
• \(c_{6} = a_{6} \text{ OP } b_{6}\);
• … and so on

Bitwise AND

In the C programming language, the bitwise AND operator, denoted as & (not to be confused with &&), is a binary operator that operates on two integer operands and returns an integer operand. The operation is performed for each pair of corresponding bits of the operands. The result is a new integer in which each bit position is set to 1 only if the corresponding bits of both operands are also 1. Otherwise, the result bit is set to 0.

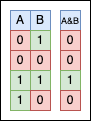
Let’s give it a try in code:

uint8_t a = 0x0Au, b = 0x0Bu;
printf("%x", a&b);

// Output
// a

Explanation: 0x0Ais 0b00001010, while 0x0B is 0b00001011, and if we were to put bits side by side and apply & between them, we would get the following:

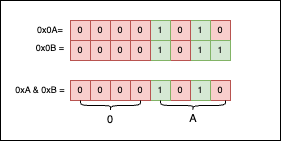
As you can see, only the 1 bits are selected, so the result is 0x0A.

Trying to apply bitwise operations to double or float types won’t work:

double a = 0.0;
printf("%x", a&1);

Error:

bits.c:120:19: error: invalid operands to binary & (have 'double' and 'double')
  120 |     printf("%x", a&1.0);
      |                   ^

One thing to take into consideration is the fact that & is both associative and commutative.

The associative property means that the grouping of operands does not affect the result. So, if we have three or more operands, we can group them in any way we choose, but the result will remain the same:

// Associativity "smoke test"
uint8_t a=0x0Au, b=0x30u, c=0x4Fu;
printf("%s\n", (((a&b)&c) == (a&(b&c))) ? "True" : "False");

// Output:
// True

Visually it’s quite an intuitive property, so let’s put a=0x0A, b=0x30, and c=0x4f side by side and see what things look like:

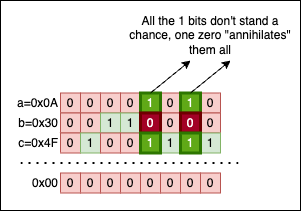
No matter how we group the operands, the results will always be the same: 0x00 because there’s no column containing only 1 bits. A single 0 in a column invalidates everything. Isn’t this demotivational?

The commutative property means that the order of operands doesn’t affect the result. So, for example, writing a&b renders the same result as writing b&a.

// Commutativity "smoke test"
uint8_t a=0x0Au, b=0x30u;
printf("%s\n", ((a&b)==(b&a)) ? "True" : "False");

// Output: 
// True

Bitwise OR

The bitwise OR (with its symbol: |) is a binary operator that compares the corresponding bits of two integer operands a produces a new value in which each bit is set to 1 if either (or both) of the corresponding bits in the operand are one.

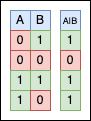
Again, let’s try using | in our code:

uint8_t a = 0xAAu, b=0x03u;
printf("%x", a|b);

// Output
// AB

Explanation 0xAA is 0b10101010, while 0x03 is 0b00000011. If you put the two numbers side by side and apply | to their bits, we get the result 0xAB. Visually, things look like this:

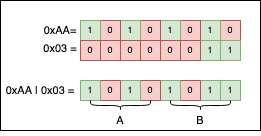
If we look at the columns, and there’s at least one bit of 1, the result on that column will be 1, regardless of the possible 0 (zeroes).

Just like &, | is both associative and commutative. Demonstrating this is outside the scope of this article, but put it like this, if there’s a single 1 on the column, no matter how many 0 bits we may encounter, the result will always be 1. A single 1 has the power to change everything. Isn’t this motivational?

Bitwise XOR

The bitwise XOR operator (^) is a binary operator that compares the corresponding bits of two operands and returns a new value where each bit is set to 1 if the corresponding bits of the operand are different, and 0 if they are the same.

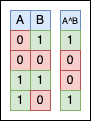
Two identical numbers, a and b, will always XOR to 0 because all the matching bits will nullify themselves.

So, if a==b then a^b==0:

uint8_t a = 0xAFu, b=0xAFu;
printf("a==b is %s\n", (a==b) ? "True" : "False");
printf("a^b=0x%x\n", a^b);

// Output
// a==b is True
// a^b=0x0

Because we like patterns, we can also use 0xAA ^ 0x55 == 0xFF, visually it’s more satisfying than any other example I could think of:

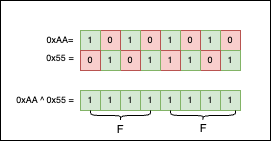
Like & and | before, ^ is an associative and commutative operation. So, another useless but interesting observation we can make is that XORing all the numbers in a loop up to a power of two (>=2) is always 0. Philosophically speaking, XOR is the killer of symmetry:

void xoring_power_two() {
    // An array containing a few powers of 2
    uint8_t pof2[4] = {4, 8, 16, 32};
    // For each power of two
    for(int i = 0; i < 4; i++) {
        uint8_t xored = 0;
        // XOR all numbers < the current power of two
        for(int j = 0; j < pof2[i]; j++) {
            printf(" 0x%x %c", j, (j!=(pof2[i]-1)) ? '^' : 0);
            xored^=j;
        }
        // Print the final result `= xored`
        printf("= 0x%x\n", xored);
    } 
}

// Output
// 0x0 ^ 0x1 ^ 0x2 ^ 0x3 = 0x0
// 0x0 ^ 0x1 ^ 0x2 ^ 0x3 ^ 0x4 ^ 0x5 ^ 0x6 ^ 0x7 = 0x0
// 0x0 ^ 0x1 ^ 0x2 ^ 0x3 ^ 0x4 ^ 0x5 ^ 0x6 ^ 0x7 ^ 0x8 ^ 0x9 ^ 0xa ^ 0xb ^ 0xc ^ 0xd ^ 0xe ^ 0xf = 0x0
// 0x0 ^ 0x1 ^ 0x2 ^ 0x3 ^ 0x4 ^ 0x5 ^ 0x6 ^ 0x7 ^ 0x8 ^ 0x9 ^ 0xa ^ 0xb ^ 0xc ^ 0xd ^ 0xe ^ 0xf ^ 0x10 ^ 0x11 ^ 0x12 ^ 0x13 ^ 0x14 ^ 0x15 ^ 0x16 ^ 0x17 ^ 0x18 ^ 0x19 ^ 0x1a ^ 0x1b ^ 0x1c ^ 0x1d ^ 0x1e ^ 0x1f = 0x0

If we picture this in our heads, this result is not surprising:

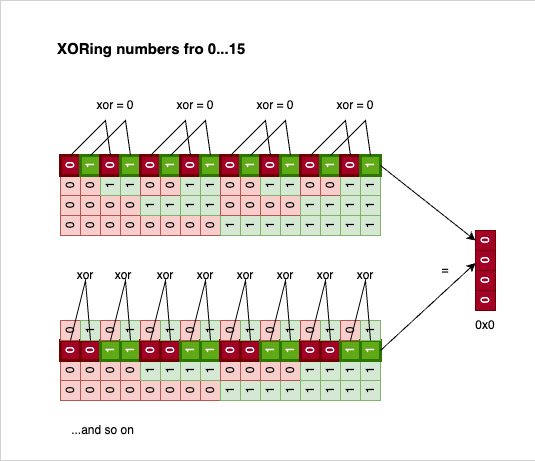
Every bit has a pair; all pairs are 0, XORing 0 with 0 is 0, and everything reduces to nothing.

Bitwise NOT

In the C Programming language, the bitwise NOT it’s a unary operator denoted by the ~ character. It works on a single operand, negating all the operand bits by changing 1 to 0 and 0 to 1.

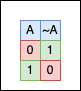
Negating 0b0001 is 0b1110, negating 0b0000 is 0b1111 and so on…

For example:

uint16_t a = 0xAAAAu; // a = 1010 1010 1010 1010 == 0xAAAA
uint16_t b = ~a;     // b = 0101 0101 0101 0101 == 0x5555
printf("0x%X\n", a);
printf("0x%X\n", b);

// Output
// 0xAAAA
// 0x5555

And visually things look like this:

Left Shift

The left shift operation is a bitwise operation, denoted with the symbols <<, that shifts the bits of a binary number to the left by a specified amount of positions.

So, for example, if we want to shift the bits of 0b0000010 (or 0x02) with three positions, we can write something like this:

uint8_t a = 0x02u;   // 0b 0000 0010 = 0x02
uint8_t b = a << 3; // 0b 0001 0000 = 0x10 
printf("After shift: 0x%x\n", b);

// Output
// After shift: 0x10

Visually things look like this:

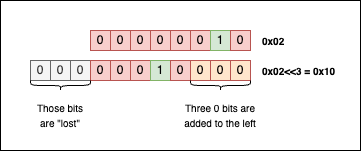
When shifting bits to the left, the bits that “fall off” the left end are lost, and the resulting bits on the right are filled with zeros.

Right Shift

The right shift operation is a bitwise operation, denoted with the symbols >>, that shifts the bits of a binary number to the right by a given amount of positions.

So for example, if we want to shift 0xAA with 4 positions, by performing 0xAA>>4 we will obtain 0x0A:

uint8_t a = 0xAAu;   // 1010 1010 = 0xAA
uint8_t b = a >> 4; // 0000 1010 - 0x0A
printf("After shift: 0x%X\n", b);

// Output
// After shift: 0xA

Visually things look like this:

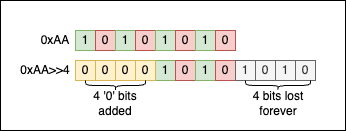
Negative numbers and their binary representation

Reading through this point, you may feel an elephant lurking in the server room. We haven’t touched on a vital subject: How are signed integers represented in binary?

In the C programming language, fixed-size signed integers are represented using Two’s Complement. The most significant bit of the number (also called MSB) is used to the sign, and the rest of the bits are used to store the number’s value. The sign bit is 0 for positive numbers and 1 for negative numbers. By convention, the number 0 is considered a positive number.

In Two’s Complement, the negative number is obtained by flipping all the bits of the positive value (~) of the number and then adding 1.

For example, to obtain the binary representation of -47, we should do the following:

1. Transform 47 in binary: 00101111;
2. We flip the bits of 47: 11010000;
3. We add 1 to the result of the previous step: 11010001.

So, -47 in binary is 11010001.

Another example. To obtain the binary representation of -36, we should do the following:

1. We transform 36 in binary: 00100100;
2. We flip the bits of 36: 11011011;
3. We add 1 to the result from the previous step: 11011100.

There’s one bit less to represent the actual numerical value for signed integers because the sign bit is reserved. The maximum positive value a int8_t can hold is: \(2^7-1=127\) and has the following representation:

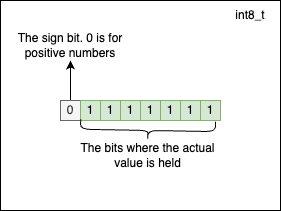
The minimum value a signed integer of type int8_t can hold is \(-2^7=128\). At this point, you may wonder why is that for negative we have -128 vs 127 for positives. This happens because 0 is considered to be positive by convention. -128 has the following representation:

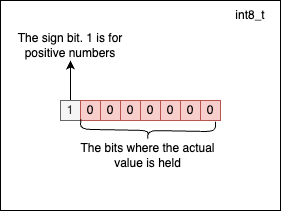
You don’t have to do any computations to determine the maximum and minimum values a signed fixed-length type can get. The limits are already defined as macro constants in "stdint.h":

#include <stdio.h>
#include <stdint.h> // constant macros are included here

int main(void) {
    printf("int8_t is in interval: [%hhd, %hhd]\n", INT8_MIN, INT8_MAX);
    printf("int16_t is in interval: [%hd, %hd]\n", INT16_MIN, INT16_MAX);
    printf("int32_t is in interval: [%d, %d]\n", INT32_MIN, INT32_MAX);
    printf("int64_t is in interval: [%lld, %lld]\n", INT64_MIN, INT64_MAX);
    return 0;
}
// Output
// int8_t is in the interval: [-128, 127]
// int16_t is in the interval: [-32768, 32767]
// int32_t is in the interval: [-2147483648, 2147483647]
// int64_t is in the interval: [-9223372036854775808, 9223372036854775807]

Just like in the previous example, it’s advisable to use the right string formats for the family of fixed-lenght signed integers: PRId8, PRId16, etc.

Pitfalls to avoid when using bitwise operations

In the C programming language, UB (a cute acronym for Undefined Behavior) refers to situations (usually corner cases, but not always) when the C Standard does not cover the expected result after executing a piece of code. In those cases, compilers can choose to do things their way by crashing, giving erroneous or platform-dependent results (worse than crashing), or trolling us with Heisenbugs. Most cases of UB are ubiquitous, while others are more subtle and hard to detect.

In the C community, undefined behaviour may be humorously called “nasal demons” after a comp.std.c post that explained undefined behaviour as allowing the compiler to do anything it chooses, even “to make demons fly out of your nose”. (source)

Just like managing the memory yourself, there are a few things that you should take into consideration when writing C code that uses bitwise operations:

A. Do not shift bits with more (or equal) than the width of the type:

uint8_t a = 32;
uint8_t b = a << 32; // undefined behavior
                     // code compiles just fine
                     // don't assume the number is 0x0

If you try to compile this simple piece of code with -Wall, the compiler (both clang and gcc) will you warn about the potential problems, but the code will still compile:

bits.c:150:19: warning: left shift count >= width of type [-Wshift-count-overflow]
  150 |     uint8_t b = a << 32; // undefined behavior

If I execute the code after compiling it, b is 0. But don’t assume it will be 0 on all platforms or with all compilers. That’s wrong.

Also, don’t rely on compiler warnings. They can only be raised in particular cases. Take a look at this code that can lead to UB:

srand(time(NULL));
uint8_t a = 32;
int shifter = rand();
uint8_t b = a << shifter;
printf("%hhu\n", b);

The code compiles without any warning and executes fine. The compiler couldn’t determine the value of the shifter at compile time, so no warning was raised. So whenever you are performing bitwise operations (especially shifts), you’d better know what you are doing.

B. Do not shift bits using negative amounts:

uint8_t a = 0x1u;
uint8_t b = a << -2; // undefined behavior
                     // code compiles just fine

C.Do not shift signed integers to cause sign changes:

int8_t a = -1;
int8_t b = a << 1; // undefined behavior
                   // code compiles just fine 

The result of E1 « E2 is E1 left-shifted E2 bit positions; vacated bits are filled with zeros. If E1 has an unsigned type, the value of the result is E1 × 2E2, reduced modulo one more than the maximum value representable in the result type. If E1 has a signed type and nonnegative value, and E1 × 2E2 is representable in the result type, then that is the resulting value; otherwise, the behavior is undefined.

Mandatory Computer Science Exercise - The solitary integer

Now that we understand the basics of bitwise operations let’s solve a classical Computer Science exercise called: The solitary integer. If you are curious, you can probably find it on leetcode and hackerrank (under the name The Lonely Integer).

The ask is straightforward:

Given an array of integer values, where all elements **but one** occur twice, 
find the unique element, the so-called _solitary_ integer. 

For example, if `L={1,2,3,3,8,1,9,2,9}`, the unique element is `8`, 
because the rest of the elements come in pairs.

The first reflex to solve this exercise would be to brute force the solution by verifying each element with every other to find its pair. But the complexity of doing so is O(n²), where n is the size of the input array - not excellent. But, as a rule of thumb, if you receive a question like this at an interview and don’t know how to approach it, mentioning the brute-force solution is a good starting point and can buy you some time until you come up with something better.

There are, of course, other alternative solutions:

• Sorting the array in O(nlogn) and then iterate through it by i+=2. If L[i]!=L[i+1], you’ve just found the lonely integer.
• Using a hashtable and count the frequency of the numbers. If the frequency of a key is 1, the problem is solved; you’ve just found the lonely integer.

But all those solutions are slightly overkill if you know about XOR. As we’ve said earlier, XOR nullifies identical bits. We also know that XOR is associative and commutative. So, why don’t we apply XOR between all the numbers? In the end, only the bits without pairs will “survive”. Those surviving bits hold the answer to our problem.

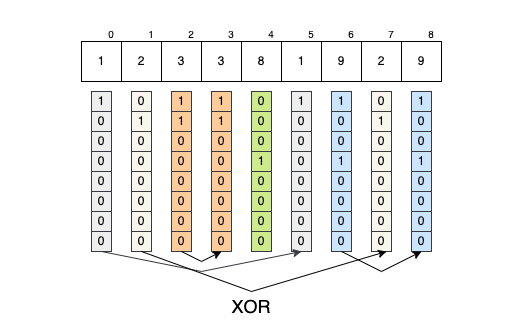
• The bits of array[0] will (eventually) nullify themselves with the bits from array[5] => array[0] ^ array[1] == 0;
• The bits of array[1] will (eventually) nullify themselves with the bits from array[7] => array[1] ^ array[7] == 0;
• The bits of array[2] will (eventually) nullify themselves with the bits from array[3] => array[2] ^ array[3] == 0;
• The bits of array[6] will (eventually) nullify themselves with the bits from array[8] -> array[6] ^ array[8] == 0;
• The bits of array[4] will remain unaltered; they represent the solution;

So, the solution of exercise becomes:

static int with_xor(int *array, size_t array_size) {
      int result = 0;
      for(int i = 0; i < array_size; ++i)
          result^=array[i];
      return result;
}
int main(void) {
    int array[9] = {1,2,3,3,8,1,9,2,9};
    printf("%d\n", with_xor(array, 9));
    return 0;
}

// Output
// 8

Printing numbers in binary by using bitwise operations

In a previous section of the article, we devised a solution to transform numbers from one numeric system to another. Chances are we will never have to convert to base 11. So why write a function that transforms a number in the binary format using bitwise operations?

The simplest solution I could think of is the following:

void print_bits_simple_rec(FILE *out, uint16_t n) {
    if (n>>1)
        print_bits_simple_rec(out, n>>1);       
    fprintf(out, "%d", n&0x1u);                  
}

print_bits_simple_rec is a recursive function that takes an uint16_t and it prints its bits. At each recursive call, we shrink the number by shifting one bit to the right (n>>1). We stop the recursive calls once the number reaches 0. After the recursive stack is built, we print the last bit of the number for each call (n&0x1).

It’s not the scope of this article to explain recursion, but let’s see how things execute if we call the function on n=0b00011011:

And then, once n=0b00000001, we start printing characters backwards:

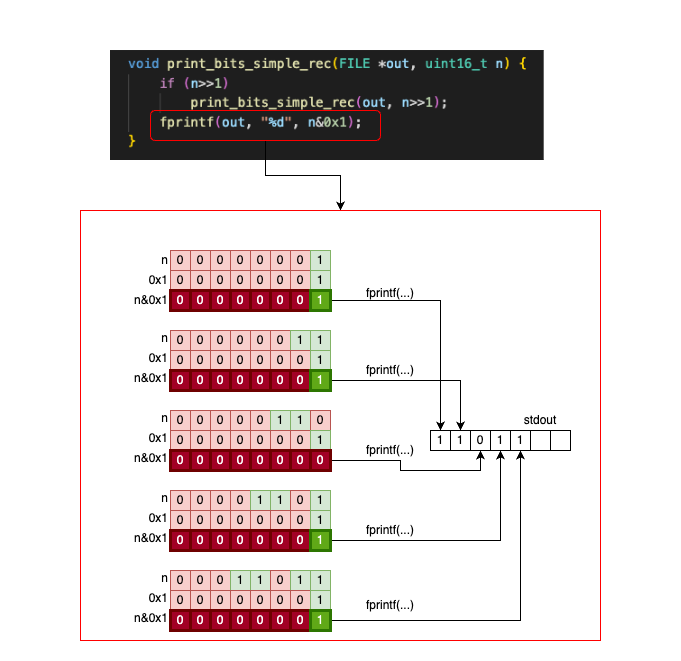
That’s one idea. Another idea is to use a value table where we keep the binary strings associated with all the binary numbers from 0 to 15:

const char* bit_rep[16] = {
    "0000", "0001", "0010", "0011",
    "0100", "0101", "0110", "0111",
    "1000", "1001", "1010", "1011",
    "1100", "1101", "1110", "1111",
};

We can then write a few functions that re-use bit_rep. For example, if we plan to print an uint8_t, all we need to do is to write this function:

void print_bits_uint8_t(FILE *out, uint8_t n) {
    fprintf(out, "%s%s", bit_rep[n >> 4], bit_rep[n & 0xF]);
}
int main(void) {
    uint8_t n = 145;
    print_bits_uint8_t(stdout, n);
}

// Output
// 10010001

This new function works like this:

• uint8_t n has 8 bits in total.
• If we split n into two halves of 4 bits each, we can use bit_rep[half1] and bit_rep[half2] to print the content of n;
• To split n into two halves, we have to:
  • n>>4 to get the first 4 bits;
  • n & 0xF to get the last 4 bits;

If you are confused about n>>4 and n & 0xF, let’s visualise what’s happening and how bits move. We will use n=145 to exemplify.

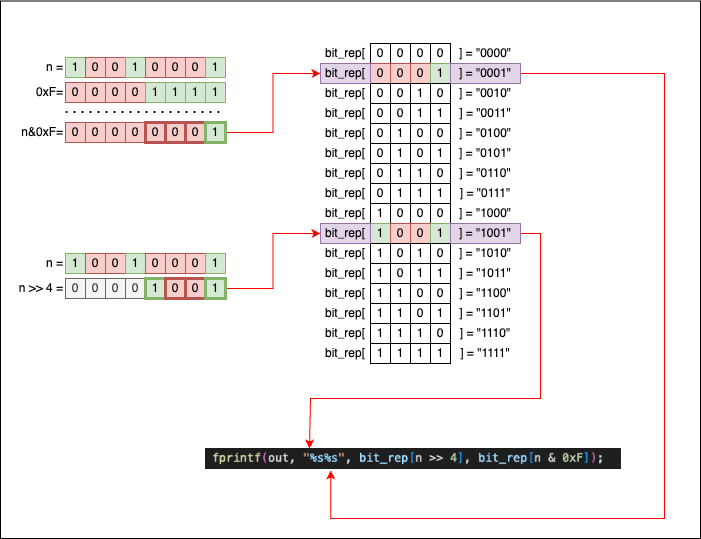
If we consider the following:

• One uint16_t variable can contain two uint8_t variables;
• One uint32_t variable can contain two uint16_t variables;
• One uint64_t variable can contain two uint32_t variables;

We can then write the following code, where each function re-uses the function of the lesser type. The idea is the same: we split the greater type into two halves and pass it to the function associated with the lesser type.

void print_bits_uint8_t(FILE *out, uint8_t n) {
    fprintf(out, "%s%s", bit_rep[n >> 4], bit_rep[n & 0xFu]);
}
void print_bits_uint16_t(FILE *out, uint16_t n) {
    print_bits_uint8_t(out, n >> 8); // first 8 bits
    print_bits_uint8_t(out, n & 0xFFu); // last 8 bits
}
void print_bits_uint32_t(FILE *out, uint32_t n) {
    print_bits_uint16_t(out, n >> 16); // first 16 bits
    print_bits_uint16_t(out, n & 0xFFFFu); // last 16 bits
}
void print_bits_uint64_t(FILE *out, uint64_t n) {
    print_bits_uint32_t(out, n >> 32); // first 32 bits
    print_bits_uint32_t(out, n & 0xFFFFFFFFu); // last 32 bits
}

Having separate functions for each type is not ideal, but prevalent in the C programming language. Fortunately, we can use the _Generic macro to group functions up.

#define print_bits(where, n) _Generic((n), \
                uint8_t: print_bits_uint8_t, \
                int8_t: print_bits_uint8_t, \
                uint16_t: print_bits_uint16_t, \
                int16_t: print_bits_uint16_t, \
                uint32_t: print_bits_uint32_t, \
                int32_t: print_bits_uint32_t, \
                uint64_t: print_bits_uint64_t, \
                int64_t: print_bits_uint64_t) \
            (where, n)

So now, we can simply call print_bits() regarding the input type (! as long as the type is covered by a _Generic macro branch):

uint8_t a = 145;
uint16_t b = 1089;
uint32_t c = 30432;
int32_t d = 3232;
print_bits(stdout, a); printf("\n"); // works on uint8_t !
print_bits(stdout, b); printf("\n"); // works on uint16_t !
print_bits(stdout, c); printf("\n"); // works on uint32_t !
print_bits(stdout, d); printf("\n"); // works on int32_t !

// Output
// 10010001
// 0000010001000001
// 00000000000000000111011011100000
// 00000000000000000000110010100000

Masking

In low-level programming, bitwise masking involves the manipulation of individual bits of a number (represented in binary) using the operations we’ve described in the previous sections (&, |, ~, ^, >>, <<). A mask is a binary pattern that extracts and manipulates specific bits of a given value.

Using bitmasking techniques, we can:

• Set a specific bit to a value (0 or 1);
• Clear a specific bit, or a bit portion from a number;
• Flip the values of all the bits of a number.
• etc.

Let’s take a look at the previously defined function, print_bits_uint8_t, that prints the binary representation of a uint8_t:

void print_bits_uint8_t(FILE *out, uint8_t n) {
    fprintf(out, "%s%s", bit_rep[n >> 4], bit_rep[n & 0xFu]);
}

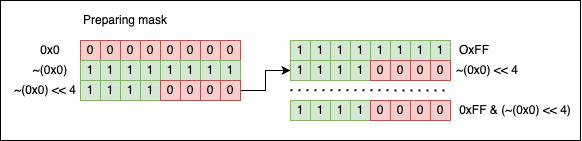
0xF is the mask we use to select the last 4 bits of n. This happens when we apply n&0xF: all the bits of 1 from the mask are used to extract information from n, and all the bits of 0 from the mask discard information from n:

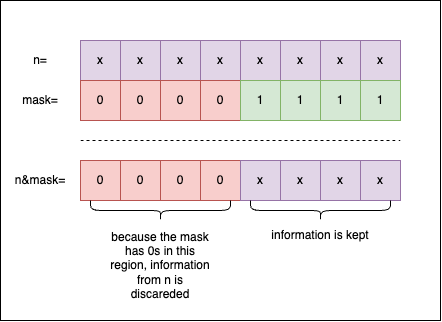
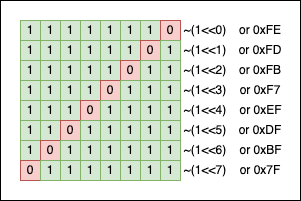
When we create the mask, we can write the pattern by hand, using hexadecimal literals, or we can express them using powers of 2. For example, if you want a simple mask for one bit on the nth position, we can write: 1<<nth. 2^nth == 1<<nth:

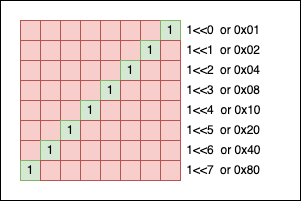
We can also “flip” the mask using the ~(mask) operation:

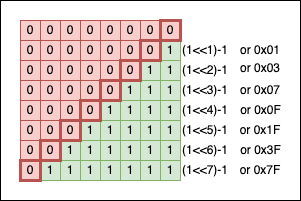
To get a “contiguous” zone of 1s, we can subtract 1 from the corresponding power of twos:

The power of masking - Pairwise Swap

In the famous book called Cracking The Coding Interview there’s one exercise where the reader is asked to swap the even bits with the odd bits inside a number:

If you ignore the ask to use as few instructions as possible our programmer’s reflex would be to:

• Keep all the bits of the number in an array;
• Perform swaps inside the array;
• Recreate the numbers based on the new array configuration.

Of course, a simpler solution uses bitwise operations and the masking technique. Spoiler alert, we will start with the actual solution, followed by some in-depth explanations:

uint16_t pairwise_swap(uint16_t n) {
    return ((n&0xAAAAu)>>1) | ((n&0x5555u)<<1);
}

Cryptic, but simple:

uint16_t n = 0xBCDDu;
uint16_t n_ps = pairwise_swap(n);
print_bits(stdout, n); printf("\n");
print_bits(stdout, n_ps); printf("\n");

// Output
// 1011110011011101
// 0111110011101110

The key to understanding the solution lies in the patterns described by the binary numbers 0xAAAA and 0x5555. 0xAAAA selects all the even bits of n, while 0x5555 selects all the odd bits of n. If we put the numbers side by side, we should see that:

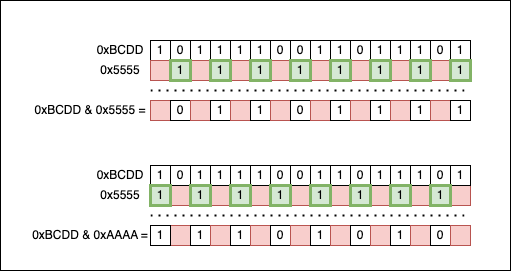
At this point, the information initially contained in the input number (n=0xBCDD) is contained in the two numbers:

• 0xBCDD & 0x5555 will contain the odd bits of 0xBCDD;
• 0xBCDD & 0xAAAA will contain the even bits of 0xBCDD;

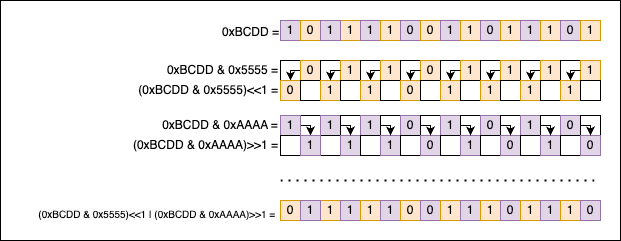
Now we need to swap them. We will shift the even bits one position to the left, and the odd bits one place to the right, so we don’t lose any. To recombine the two interlacing patterns back, we use the | operation.

Getting, Setting, Clearing, Toggling the nth bit

Getting the nth bit of a number

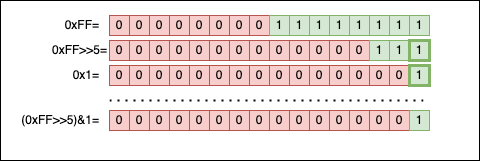
To get the nth bit of a number n, we can use the & and >> bitwise operations:

• We shift the number >> with nth positions;
• We apply a simple mask to &0x1 for obtaining the last bit;

Most online resources (ChatGPT included) will recommend you the following two solutions for retrieving the nth bit:

A macro:

#define GET_BIT(n,pos) (((n)>>(pos))&1)

Or a method:

int get_bit(int num, int n) {
    return (num >> n) & 0x1u;
}

Visually, both solutions work like this:

I prefer using a method instead of a macro, depending on the context. It’s best to validate the input and ensure n is not negative or bigger than the size (in bits) of num. Otherwise, things can lead to UB fast:

inline uint8_t get_nth_bit(uint32_t num, uint32_t nth) {
    if (nth>=32) {
        // Catch error
        // Log & Manage the error
    }
    return (num>>nth)&0x1u;
}

Let’s try it in practice now:

int main(void) {
    uint32_t n = 0xFFu;
    int i = 0;   
    printf("Printing last 8 bits:\n");
    for(; i < 8; i++)
        printf("%hhu", get_nth_bit(n,i));
    printf("\nPriting the first 24 bits:\n");
    for(; i < 32; i++) 
        printf("%hhu", get_nth_bit(n,i));
}

// Output
// Printing last 8 bits:
// 11111111
// Printing the first 24 bits:
// 000000000000000000000000

Setting up the nth bit of a number

The bit of a number n can be set to 0 or 1, and depending on the context, we can end up having two functions or macros:

#define set_nth_bit1(num, pos) ((num) |= (1 << (pos)))
#define set_nth_bit0(num, pos) ((num) &= ~(1 << (pos)))

// Or functions

inline void set_nth_bit0(uint32_t *n, uint8_t nth) {
    *n &= ~(1u << nth);
}
inline void set_nth_bit1(uint32_t *n, uint8_t nth) {
    *n |= (1u << nth);
}

Because both of the functions (and macros) can lead to UB, it’s advisable to validate nth to make sure it’s not bigger than the length (in bits) of the type of n (in our case it’s uint32_t, so it should be smaller < than 32).

Using the functions in code:

uint32_t n = 0x00FFu;
print_bits(stdout, n); printf("\n");

set_nth_bit0(&n, 5);
printf("bit 5 of n is: %hhu\n", get_nth_bit(n, 5));
print_bits(stdout, n); printf("\n");

set_nth_bit1(&n, 5);
printf("bit 5 of n is: %hhu\n", get_nth_bit(n, 5));
print_bits(stdout, n); printf("\n");

// Output
// 00000000000000000000000011111111
// bit 5 of n is: 0
// 00000000000000000000000011011111
// bit 5 of n is: 1
// 00000000000000000000000011111111

Visually, set_nth_bit0 looks like this:

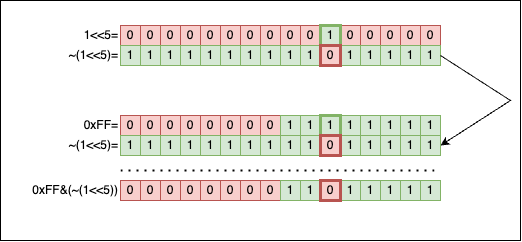
Applying & between 0 and 1 will always return 0. So we create a mask for the 5th bit (1<<5), we flip it (~(1<<5)) so we get a 0 on the 5th position, and then we apply & (bitwise AND). The 1 doesn’t stand a chance.

Visually, set_nth_bit1 looks like this:

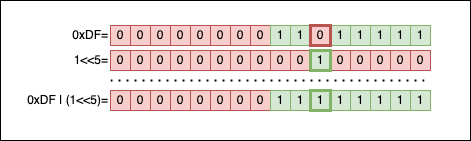
Applying | between 0 and 1 returns 1. So we create a mask for the 5th bit (1<<5), then apply | between the mask and the number to fix the gap.

Toggling the nth bit of a number

Toggling the bit of the number means changing the value of a specific bit from 0 to 1 or from 1 to 0 while leaving all the other bits unchanged.

The first reflex would be to re-use the previously defined functions set_nth_bit1(...) and set_nth_bit0(...) to improvise something like:

void toggle_nth_bit(uint32_t *n, uint8_t nth) {
    if (get_nth_bit(n,nth)==0) {
        set_nth_bit1(n, nth);
    } else {
        set_nth_bit0(n, nth);
    }
}

But there’s a better and simpler way that avoids branching altogether and uses XOR:

void toggle_nth_bit(uint32_t *n, uint8_t nth) {
    *n ^= (1u<<nth);
}

The idea is quite simple; we create a mask with 1 on the nth position (1<<nth), and then we ^ (XOR) the number n with the mask. This will preserve all the bits of n, minus the nth bit will change values depending on its state (it will toggle).

Let’s visualise this, by imagining calling: toggle_nth_bit(0xF0u, 3):

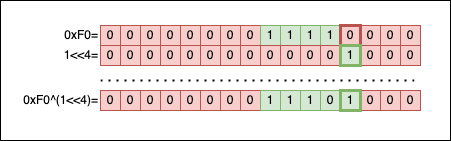
The result of toggle_nth_bit(0xF0u, 3) should be 0xF8:

uint32_t n = 0xF0u;
toggle_nth_bit(&n, 3);
if (n==0xF8u) {
    printf("It works!");
}

// Output
// It works!

Or we perform the inverse operation on the same bit:

uint32_t n = 0xF8u;
toggle_nth_bit(&n, 3);
if (n==0xF0u) {
    printf("It works!");
}

// Output
// It works!

Getting, Setting, Clearing, and Toggling a bit portion of a number

Clearing the last bits of a number

So let’s say we have a number n. Our task is to write a generic method that clears the last nbits of that number.

The solution is simple:

• We need to create a mask where all the bits are 1, except the last nbits, which are 0.
• We apply an & operation between n and the newly created mask;

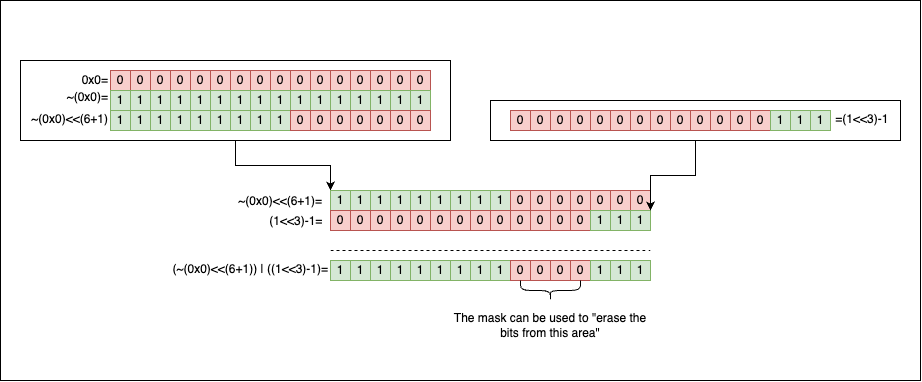
To create the mask, we start from a value where all the bits are set to 1. This value can be easily obtained by flipping all the bits of 0: ~0x0u. Next, we left shift with nbits and, voila, the mask is ready.

The code is:

void clear_last_bits(uint32_t *n, uint8_t nbits) {
    *n &= (~(0x0u) << nbits);
}

To test it, let’s try to clear the last 4 bits of 0xFF. The result should be: 0xF0:

uint32_t n = 0xFFu;
clear_last_bits(&n, 4);
if (n==0xF0u) {
    printf("It works!\n");
}

// Output
// It works!

Visually, the operation looks like this:

Replacing multiple bits

In this case, the ask is simple; given an uint16_t and two bit indices, i and j, we need to write a method that replaces all the bits between i and j (including j) from N with the value of M. In other words, M becomes a substring of N that starts at i and ends at j.

The signature of the method should be the following:

void replace_bits(uint32_t *n, uint32_t m, uint8_t i, uint8_t j);

A simple solution that doesn’t impose any validation on i, j or m can be:

void replace_bits(uint16_t *n, uint16_t m, uint8_t i, uint8_t j) {
    // Creates a mask to clear the bits from i to j inside N
    // The mask is made out of two parts that are stitched together using 
    // a bitwise OR
    uint16_t mask = (~0x0u << (j+1)) | ((1<<i)-1);
    // Clear the bits associated with the mask
    *n &= mask;
    // Align the bits to be replaced
    m <<=i;
    // Replace the bits from n with the value of m
    *n |= m;
}

Executing the code:

uint16_t n = 0xDCBEu;
print_bits(stdout, n); printf("\n");
replace_bits(&n, 0x1u, 3, 6);
print_bits(stdout, n); printf("\n");

// Output
// 1101110010111110
// 1101110010001110

As you can see, the bits from positions 3 to 6 (inclusive) were replaced with the value of 0x1, which is 0b001 in binary.

To understand what’s happening behind the scenes, we should go through the algorithm step by step.

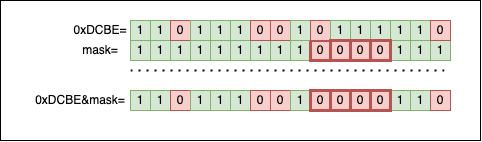
Firstly we need to build a mask that selects the interval defined by i and j. The mask will be created by stitching together the two sections (using |). The line of code where we create the mask is: uint16_t mask = (~0x0u << (j+1)) | ((1<<i)-1);. Visually it works like this:

The second step is to use the resulting mask to clear the bits from i to j (including j) inside n: *n &= mask;:

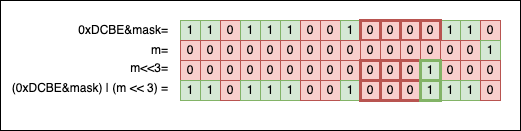
The third step is to shift the bits of m with i positions to the left to align them with the empty portion created by the mask. And then use m as a new mask: *n |= m;:

Reading multiple bits

Reading multiple bits (instead of replacing them) is a similar task to the one described above. We must write a method that works on an uint16_t and two bit indices i and j. We need to extract and return the value of all the bits between i and j (including j).

A proposed C function might look like this:

uint16_t get_bits(uint16_t input, uint8_t i, uint8_t j) {
    uint16_t mask = (1u << (j - i + 1)) - 1;
    mask <<= i;
    return (input & mask) >> i;
}

Or, if we enjoy confusing our colleagues, we can try something like this:

uint16_t get_bits2(uint16_t input, uint8_t i, uint8_t j) {
    uint16_t mask = (1u << (j + 1)) - (1 << i);
    return (input & mask) >> i;
}

When we try them in practice, magic unfolds:

uint16_t n = 0xDCBE;
print_bits(stdout, n); printf("\n");
replace_bits(&n, 0x7u, 3, 6);
print_bits(stdout, n); printf("\n");
print_bits(stdout, get_bits(n, 3, 6)); printf("\n");
print_bits(stdout, get_bits2(n, 3, 6)); printf("\n");

// Output
// 1101110010111110
// 1101110010111110
// 0000000000000111
// 0000000000000111

It all boils down to how we’ve decided to implement the masking mechanisms:

• uint16_t mask = (1u << (j - i + 1)) - 1; mask <<= i; // OR
• uint16_t mask = (1u << (j + 1)) - (1u << i);

As you can see, in both versions (get_bits and get_bits2), we’ve decided to create the mask in one go without stitching together two sections as we did in replace_bits.

Let’s take the first version to exemplify further. If we look closer, there’s no magic involved.

(1 << (j - i + 1))      -1
------------------
   power of two         -1

That’s a power of two from which we subtract 1. We know the bit pattern associated with that kind of number (\(2^n-1\)):

So, visually speaking, the mask forms like this:

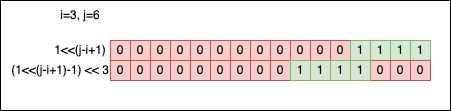
• j-i+1 gives the length of the mask (the contiguous zone of 1 bits);
• The second shift mask <<= i put 1 bits to the right position.

Bitwise operations and their relationship with the powers of two

There’s a strong relationship between bitwise operations and mathematical operations involving powers of two. This happening shouldn’t be any mystery or a surprise; after all, we use the powers of two to represent the number in the binary system.

Multiplying a number with a power of two

Multiplying a number \(a\) with a power of two, \(a * 2^{n}\), is equivalent to writing a<<n, shifting the bits of a to the right with n positions.

There’s a clear mathematical demonstration for this. If we go back to the beginning of the article and re-use the formula stated there, we know a number in the binary system can be written as a sum of the power of twos: \(A_{2} = \sum_{i=0}^{n} a_i * 2^i\), where \(a_{i} \in \{0, 1\}\). If we multiply both sides of the relationship with \(2^m\), the relationship becomes:

\[2^{m} * A_{2} = \sum_{i=0}^{n} a_i * 2^{i+m}\]

We can intuitively understand that the first m bits of information were lost, now when we sum; we don’t start with \(2^0\) anymore, but rather with \(2^{m}\), so that:

\[2^{m} * A_{2} = a_{0} * 2^{m} + a_{1} * 2^{m+1} + a_2*2^{m+2} + ... + a_{n} * 2^{n+m}\]

So, if we were to link the mathematical formula with what’s happening at the bit level, let’s take a look at the following picture:

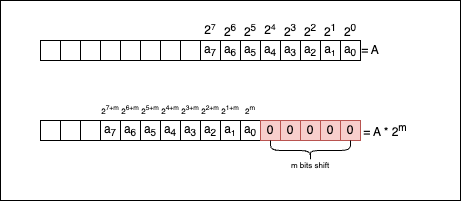
Now let’s see if the compiler knows how to optimise the multiplication without explicitly telling it so. Given the following code:

int main(void) {
    srand(0);
    int i = rand();
    for(; i < (1<<12); i*=4) {
        printf("%d\n", 1);
    }
    return 0;
}

You can see that instead of writing i<<=2 in the loop, we’ve preferred to use the more readable i*=4. If we compile the code (gcc -O3 for x86-64) and look at the resulting assembly:

.LC0:
        .string "%d\n"
main:
        push    rbx
        xor     edi, edi
        call    srand
        call    rand
        cmp     eax, 4095
        jg      .L2
        mov     ebx, eax
.L3:
        mov     esi, 1
        mov     edi, OFFSET FLAT:.LC0
        xor     eax, eax
        ; Shifts the value in ebx to the left by 2 bits (multiplication by 4)
        sal     ebx, 2
        call    printf
        cmp     ebx, 4095
        jle     .L3
.L2:
        xor     eax, eax
        pop     rbx
        ret

You will see the compiler is smart enough to detect that one of the operands of i*=4 is a power of two, so it uses the equivalent >> instruction, which is sal ebx, 2, where:

• sal is an instruction that stands for shift arithmetic left;
• ebx is the register where our i value is kept;
• 2 is the number of positions we shift to.

Compilers can perform this optimisation for you, so you shouldn’t bother.

Dividing a number with a power of two

Dividing a number \(a\) with a power of two, \(a \div 2^{n}\), is equivalent to writing a>>n. The mathematical demonstration is identical to the multiplication one so we won’t write it here.

But we can perform the following smoke test:

uint16_t a = 100u;
if (a/2 == a>>1) {
    printf("Yes, we are right\n");
}

// Output
// Yes, we are right

Now let’s look at the following code:

int main(void) {
    srand(NULL);
    uint32_t n = rand(); // generates a random number
    while(n!=0) {        // while the number is different than 0
        n /=2;           // we divide it with 2 
    }
    return 0;
}

If we compile the code with gcc -O1 (for x86-64), the resulting assembly code is:

main:
        sub     rsp, 8
        mov     edi, 0
        call    srand
        ; Generate a random number and store the result in eax
        call    rand
        ; Test if the random number is 0 . 
        ; If it is jump to .L2 otherwise continue
        test    eax, eax
        je      .L2
.L3:
        ; Copy the value of eax to edx
        mov     edx, eax
        ; Shift the value of eax to the right with 1 position
        shr     eax
        ; Compare the original in edx to 1 and jump back to .L3
        cmp     edx, 1
        ja      .L3
.L2:
        mov     eax, 0
        add     rsp, 8
        ret

The important line here is shr eax, where the compiler shifts the eax one position to the right. Why did it do that? Our C code explicitly called division n /=2;. Well, the compiler realised that the operand is 2, and there’s no reason to use division instead of simple >>.

Fun fact, if we rewrite the C code with the bitwise optimisation by replacing the line n/=2 with the line n>>=1, the resulting assembly code will be identical. Compilers can perform this optimisation for you, so you should rarely bother with mundane optimisations like this.

Checking if a number is even or odd

Suppose we contemplate the following formula, where a number can be written as: \(A_{2} = \sum_{i=0}^{n} a_i * 2^i\), where \(a_{i} \in \{0, 1\}\), we will soon realise that: if we sum up powers of two in general (except \(2^{0}\)), \(A_{2}\) will always be even. A sum of even numbers is always even (we can use \(2\) as a common factor).

So the only indicator that gives the parity of the number is \(a_{0}*2^{0}\). \(a_{0}\) is the least significant bit, but in another way, it’s quite a critical fellow because it provides us with the answer to one crucial question: is the number even, or is it odd?

The rule is the following:

• If \(a_{0}=1\), thus activating \(2^{0}\), then the number is odd;
• If \(a_{0}=0\), thus deactivating \(2^{0}\), then the number is even;

So to check the parity of a number is enough to mask it with 0x1, and get the last bit:

uint16_t a = 15u;
uint16_t b = 16u;
printf("a=%d is %s\n", a, a&0x1u ? "odd" : "even");
printf("a=%d is %s\n", b, b&0x1u ? "odd" : "even");

// Output
// a=15 is odd
// a=16 is even

Getting the remainder when we divide with a power of two

The modulo operation % is slow no matter the hardware architecture we are using. So whenever we can replace it with something more efficient, it’s advisable, even if compilers can theoretically optimise things like this for you.

As a rule (a % (1<<n)) is equivalent to (a & ((1<<n)-1)), where 1<<n is the bitwise of saying \(2^n\).

If we go back to the formula, \(A_{2} = \sum_{i=0}^{n} a_i * 2^i\), where \(a_{i} \in \{0, 1\}\) and we divide into both sides with a power of two, \(2^m\), we will obtain:

\[\frac{A}{2^{m}} = a_{0} * \frac{1}{2^m} + a_{1} * \frac{1}{2^{m-1}} + a_2*\frac{1}{2^{m-2}} + ... + a_{n-1}*2^{n-m-1} + a_{n} * 2^{n-m}\]

But at some point, the denominator of the fraction \(\frac{1}{2^{m-j}}\) will become negative again so that things will turn upside down yet again. This will happen when \(j \ge m\). So, for example, if m = 3, we can write things like:

\[\frac{A}{2^3} = \underbrace{a_{0} * \frac{1}{2^3} + a_{1} * \frac{1}{2^2} + a_{2} * \frac{1}{2^1}}_\text{the bits composing the remainder} + \underbrace{a_{3} * 2^0 + a_4 * 2^1 + ... + a_{n} * 2^{n-3}}_{\text{The new bits composing }\frac{A}{2^3}}\]

So to get the remainder, we need to select the last 3 bits (with the mask ((1<<3)-1)) of the number:

uint16_t pow2 = 1u << 3;
for(int i = 1; i < 100; i++) {
    printf("%2d mod %d=%d  %c", 
        i, pow2, i & (pow2-1), i&0x7 ? ' ' : '\n');
}

// Output
//  1 mod 8=1    2 mod 8=2    3 mod 8=3    4 mod 8=4    5 mod 8=5    6 mod 8=6    7 mod 8=7    8 mod 8=0  
//  9 mod 8=1   10 mod 8=2   11 mod 8=3   12 mod 8=4   13 mod 8=5   14 mod 8=6   15 mod 8=7   16 mod 8=0  
// 17 mod 8=1   18 mod 8=2   19 mod 8=3   20 mod 8=4   21 mod 8=5   22 mod 8=6   23 mod 8=7   24 mod 8=0  
// 25 mod 8=1   26 mod 8=2   27 mod 8=3   28 mod 8=4   29 mod 8=5   30 mod 8=6   31 mod 8=7   32 mod 8=0  
// 33 mod 8=1   34 mod 8=2   35 mod 8=3   36 mod 8=4   37 mod 8=5   38 mod 8=6   39 mod 8=7   40 mod 8=0  
// 41 mod 8=1   42 mod 8=2   43 mod 8=3   44 mod 8=4   45 mod 8=5   46 mod 8=6   47 mod 8=7   48 mod 8=0  
// 49 mod 8=1   50 mod 8=2   51 mod 8=3   52 mod 8=4   53 mod 8=5   54 mod 8=6   55 mod 8=7   56 mod 8=0  
// 57 mod 8=1   58 mod 8=2   59 mod 8=3   60 mod 8=4   61 mod 8=5   62 mod 8=6   63 mod 8=7   64 mod 8=0  
// 65 mod 8=1   66 mod 8=2   67 mod 8=3   68 mod 8=4   69 mod 8=5   70 mod 8=6   71 mod 8=7   72 mod 8=0  
// 73 mod 8=1   74 mod 8=2   75 mod 8=3   76 mod 8=4   77 mod 8=5   78 mod 8=6   79 mod 8=7   80 mod 8=0  
// 81 mod 8=1   82 mod 8=2   83 mod 8=3   84 mod 8=4   85 mod 8=5   86 mod 8=6   87 mod 8=7   88 mod 8=0  
// 89 mod 8=1   90 mod 8=2   91 mod 8=3   92 mod 8=4   93 mod 8=5   94 mod 8=6   95 mod 8=7   96 mod 8=0  
// 97 mod 8=1   98 mod 8=2   99 mod 8=3

Determining if an integer is a power of two

Without taking bitwise operations into consideration, our first reflex to check if a number is a power of two is to use logarithms. It’s not the best solution, and you will shortly see why:

#include <math.h>

int is_power_of_two(int num) {
    // Negative numbers are not power of two
    // 0 is not a power of two
    if (num <= 0) {
        return 0; 
    }
    // We compute the logarithm 
    double log2num = log2(num);
    // We check if the logarithm is an integer
    return (log2num == floor(log2num));
}

Code looks fine, but it contains a dangerous comparison between log2num==floor(log2num). The reason it’s dangerous is that double numbers cannot be represented with exact precision, errors by approximation can build up, and subtle differences can appear rendering the comparison useless.

If you don’t believe me, let’s try the following code:

double x = 10 + 0.1 + 0.2 + 0.2; // should be 10.5
double y = 11 - 0.2 - 0.2 - 0.1; // should be 10.5
printf("x and y are%sequal\n", x == y ? " " : " not ");
printf("the difference between the numbers is: %1.16f\n", x-y);

// Output
// x and y are not equal
// the difference between the numbers is: -0.0000000000000036

A disputed strategy of solving this is to introduce an epsilon (a very small value representing tolerance) and compare doubles by approximating equality. So instead of making the comparison (x==y) directly, we can compare their difference with epsilon.

double epsilon = 0.000001;
if (fabs(x-y) <= epsilon) {
    // the numbers are equal or almost equal
}

This doesn’t solve the problem by itself, but it can greatly reduce the number of errors we get. So why don’t we implement this the professional way. A simple bitwise trick that determines if a number is a power of two is to write a function like this:

bool is_pow2(uint16_t n) {
    return (n & (n-1)) == 0;
}

And when we test it we saw that everything looks fine:

uint16_t a = 1u<<2, 
         b = 1u<<3, 
         c = (1u<<3) + 1;

printf("%hu is a power of two: %s.\n", a, is_pow2(a) ? "yes" : "no");
printf("%hu is a power of two: %s.\n", b, is_pow2(b) ? "yes" : "no");
printf("%hu is a power of two: %s.\n", c, is_pow2(c) ? "yes" : "no");       

// Output
// 4 is a power of two: yes.
// 8 is a power of two: yes.
// 9 is a power of two: no.

Spoiler Alert the function has one subtle bug: it doesn’t behave correctly when n is 0. Let’s try it:

uint16_t a = 0x0u;
printf("%hu is a power of two: %s.\n", a, is_pow2(a) ? "yes" : "no");

// Output
// 0 is a power of two: yes.

Mathematicians will say: Raising any non-zero number to a natural power will never result in 0. So our code should be re-written as such to consider this corner case:

bool is_pow2(uint16_t n) {
    return n && !(n & (n-1));
}

Now that things are sorted let’s take a look and see why the function works. Firstly, we all know that a number which is a power of two, in its binary representation has exactly one bit of 1 on the power’s column:

When we subtract 1 from a power of two, the bit pattern looks like this:

So if we put those two pictures side by side, we should see how things are going:

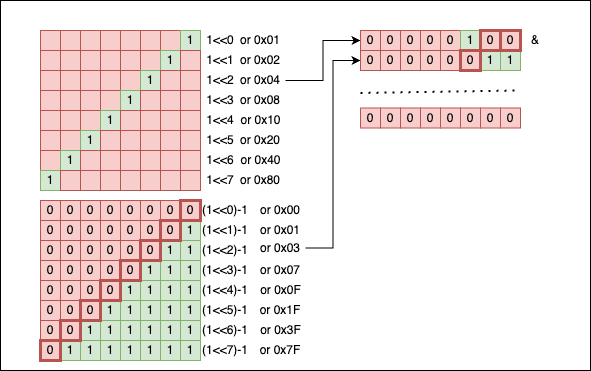
We can see that all the bits nullify themselves when we apply &. If only one bit would be different (when the number is not a power of two), this trick won’t work.

Getting the next power of two

There are cases in code when, given a number n, you want to determine the first power of two that is greater than n. For example, if n=7, the next power of two bigger than n is 8. Or, if n=13, the next power of two bigger than 13 is 16.

The programmer’s reflex would be to write a function like:

uint32_t next_power_of_two_naive(uint32_t n) {
    uint32_t r = 1u;
    while(r<x) 
        r*=2; // or r<<=1
    return r;
}

Code works, but it’s prone to errors:

uint32_t n1=0u, n2=128u, n3=7u, n4=UINT32_MAX; 
printf("next power of two for %u is %u\n", n1, next_power_of_two_naive(n1));
printf("next power of two for %u is %u\n", n2, next_power_of_two_naive(n2));
printf("next power of two for %u is %u\n", n3, next_power_of_two_naive(n3));
printf("next power of two for %u is %u\n", n4, next_power_of_two_naive(n4));

// Output
// next power of two for 0 is 1
// next power of two for 128 is 128
// next power of two for 7 is 8
// ^C <--- HAD TO CLOSE THE PROGRAM, INFINITE LOOP

Let’s abandon this solution and try to make use of bitwise operations. The new code should be like this:

uint32_t next_power_of_two(uint32_t n) {
    n--; 
    n |= n >> 1; 
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8;
    n |= n >> 16;
    n++; 
    return n;
}

Does it work better ?

uint32_t n1=0u, n2=128u, n3=7u, n4=UINT32_MAX; 
printf("next power of two for %u is %u\n", n1, next_power_of_two(n1));
printf("next power of two for %u is %u\n", n2, next_power_of_two(n2));
printf("next power of two for %u is %u\n", n3, next_power_of_two(n3));
printf("next power of two for %u is %u\n", n4, next_power_of_two(n4));

// Output
// next power of two for 0 is 0
// next power of two for 128 is 128
// next power of two for 7 is 8
// next power of two for 4294967295 is 0

Well, at least the code doesn’t enter an infinite loop when n=UINT32_MAX, but returns erroneous results for 0. So we can definitely change something to it:

uint32_t next_power_of_two(uint32_t n) {
    if (n==0) return 1; // takes care of the special case
    n--; 
    n |= n >> 1; 
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8;
    n |= n >> 16;
    n++; 
    return n;
}

Now, we should also do something when the numbers are getting closer to UINT32_MAX. As you probably know, UINT32_MAX is not a power of two (it’s actually (1<<32)-1), so searching for the next power of two, after 1<<31, doesn’t make any sense. If we let the function in the current form:

uint32_t n1=(1u<<31)+1, 
            n2=(1u<<31)+2, 
            n3=(1u<<31)+3;

printf("next power of two for %u is %u\n", n1, next_power_of_two(n1));
printf("next power of two for %u is %u\n", n2, next_power_of_two(n2));
printf("next power of two for %u is %u\n", n3, next_power_of_two(n3));

// Output
// next power of two for 2147483649 is 0
// next power of two for 2147483650 is 0
// next power of two for 2147483651 is 0

All the results will be 0. So we should branch the function again and decide on what we’re going to do when n>(1<<31).

But now let’s get back to this magic, and see what’s happening:

n--; 
n |= n >> 1; 
n |= n >> 2;
n |= n >> 4;
n |= n >> 8;
n |= n >> 16;
n++; 

Let’s assume n=0x4000A8CC (or n=1073785036). Calling next_power_of_two(0x4000A8CC) will return 0x80000000:

n        = 01000000000000001010100011001100 (0x4000A8CC)
n--      = 01000000000000001010100011001011 (0x4000A8CB)

n>>1     = 00100000000000000101010001100101
n        = 01000000000000001010100011001011
n|(n>>1) = 01100000000000001111110011101111
           -->1s                      1s<--

n>>2     = 00011000000000000011111100111011
n        = 01100000000000001111110011101111
n|(n>>2) = 01111000000000001111111111111111
           --->1s                    1s<---

n>>4     = 00000111100000000000111111111111
n        = 01111000000000001111111111111111
n|(n>>4) = 01111111100000001111111111111111
           ----->1s               1s<------

n>>8     = 00000000011111111000000011111111
n        = 01111111100000001111111111111111
n|(n>>8) = 01111111111111111111111111111111
           ------->1s           1s<--------

n>>16    = 00000000000000000111111111111111
n        = 01111111111111111111111111111111
n|(n>>8) = 01111111111111111111111111111111
           --------->1s        1s<---------

n++      = 10000000000000000000000000000000 (0x80000000)

As you can see, at each iteration, we are slowly creating a mask (in the form (1<<n)-1). By the end, when adding 1, we get the next power of two: 1<<n.

Implementing a BitSet (or BitVector)

BitSet or BitVector are used interchangeably to refer to a data structure representing a collection of bits, each of which can be 0 or 1. A BitSet is like a massive panel with ON/OFF switches. You can alter the state of those ON/OFF switches if you know their position (index in the set).

However, there can be some differences in the implementation and usage of the two terms based on the context they are being used. Sometimes, A BitSet may refer to a fixed-sized collection of bits, while BitVector may refer to a dynamically resizable collection of bits.

For simplicity, we will implement a BitSet using, you’ve guessed it, bitwise operations. The minimal set of operations a BitSet should support are:

• Setting a bit to 0 (already covered here);
• Setting a bit to 1 (already covered here);
• Retrieving the value of the bit (already covered here);
• Resetting the BitSet (setting all the bits to 0).

Now that we know how to manipulate the individual bits of an integer, we can say that:

• a uint16_t can be considered a BitSet with a size of 16;
• a uint32_t can be considered a fixed-sized BitSet with a size of 32;
• a uint64_t can be considered a fixed-sized BitSet with a size of 64;

But what if we want a BitSet with a size bigger than 64? We don’t have uint128_t (yet!). So we will probably have to use 4 uint32_t or 2 uint64_t. So a BitSet is an array of fixed-sized numbers (uintN_t), where we index bits by their relative position in the BitSet.

The following diagram describes an array of 4 uint32_t integers with a total of 4*32 ON/OFF switches (bits 0 or 1). Each bit should be accessible relative to their position in the array, not to the relative position in their integer (words):

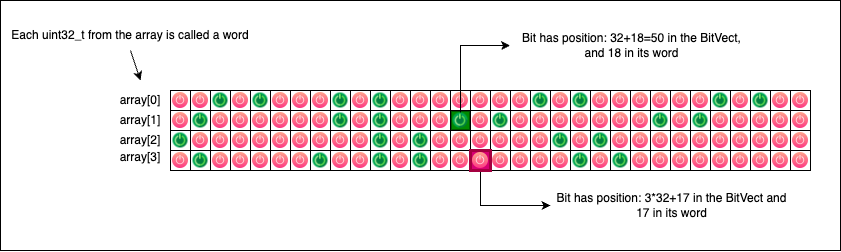
To implement the BitSet we will use C macros:

#define SET_NW(n) (((n) + 31) >> 5)
#define SET_W(index) ((index) >> 5)
#define SET_MASK(index) (1U << ((index) & 31))

#define SET_DECLARE(name, size) uint32_t name[SET_NW(size)] = {0}
#define SET_1(name, index) (name[SET_W(index)] |= SET_MASK(index))
#define SET_0(name, index) (name[SET_W(index)] &= ~SET_MASK(index))
#define SET_GET(name, index) (name[SET_W(index)] & SET_MASK(index))

Things can look daunting at first, so let’s take each line and explain what it does.

SET_NW

#define SET_NW(n) (((n) + 31) >> 5)

This macro can determine the number of uint32_t words we need to represent a BitSet of a given size.

If for example, we need 47 positions, then SET_NW(47) will return (47+31)>>5, which is equivalent to saying (47+31)/32=2. Our array needs at least two uint32_t integers to hold 47 values.

SET_W

#define SET_W(index) ((index) >> 5)

This macro returns the index of the uint32_t word that contains the bit we are looking for at the given index.

For example, if our BitSet has 64 indices (2 uint32_t words), calling SET_W(35) will return 35>>5, which is equivalent to saying 35/32=1. So we must look for the bit in the second uint32_t.

SET_MASK

#define SET_MASK(index) (1U << ((index) & 31))

Based on a given index, this returns the mask to select that individual bit from the uint32_t word. index & 31 is equivalent to saying index % 32.

So, if, for example, we call SET_MASK(16) it will create a mask that selects the bit 16 from the corresponding uint32_t word. If we call SET_MASK(35), it will create a mask that selects the bit 3 from the corresponding uint32_t word.

SET_MASK works at the word level, while SET_W works at the array level.

SET_DECLARE

#define SET_DECLARE(name, size) uint32_t name[SET_NW(size)] = {0};

This macro declares a bitset array (uint32_t[]) with the given name and size, and initializes it to all zeros. After declaration, the BitSet is a clean state, no ON/OFF switch is activated.

SET_1 and SET_0

#define SET_1(name, index) (name[SET_W(index)] |= SET_MASK(index))
#define SET_0(name, index) (name[SET_W(index)] &= ~SET_MASK(index))

Those macros can be used to SET to 0 or 1 specific bits inside the BIT_VECT. The techniques for doing this were already described here.

SET_GET

#define SET_GET(name, index) (name[SET_W(index)] & SET_MASK(index))

This macro is used to check whether a bit is a set. If the bit is set to 1, the macro returns a non-zero value. If the bit is set to 0, the macro returns 0.

Using the BitSet

To test the newly defined “macro” BitSet we can use this code:

// Declares uint32_t bitset[3] = {0};
SET_DECLARE(bitset, 84);

// Sets the bits 1 and 80 to 1
SET_1(bitset, 1);
SET_1(bitset, 80);

printf("Is bit %d set? Answer: %s.\n", 1, SET_GET(bitset, 1) ? "YES" : "NO");
printf("Is bit %d set? Answer: %s.\n", 2, SET_GET(bitset, 2) ? "YES" : "NO");
printf("Is bit %d set? Answer: %s.\n", 80, SET_GET(bitset, 80) ? "YES" : "NO");

//Output
// Is bit 1 set? Answer: YES.
// Is bit 2 set? Answer: NO.
// Is bit 80 set? Answer: YES.

Swapping two numbers

This bitwise trick is generally uncalled for, but it’s nice to use when you want to deceive your naive colleagues.

Swapping the value of two variables is normally done using an intermediary variable. This is one of the first “algorithms” we learn when we start programming:

void swap(int *a, int *b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

int main(void) {
    int a = 5, b = 7;
    printf("Before swap: a=%d b=%d\n", a,b);
    swap(&a, &b);
    printf("After swap: a=%d b=%d\n", a,b);
    return 0;
}

But there are two other ways of achieving the same result without the need to introduce a new variable, tmp:

void swap_xor(uint8_t *a, uint8_t *b) {
    *a ^= *b;
    *b ^= *a;
    *a ^= *b;
}

int main(void) {
    uint8_t a = 7u;
    uint8_t b = 13u;
    printf("Before swap: a=%hhu b=%hhu\n", a, b);
    swap_xor(&a, &b);
    printf("After swap: a=%hhu b=%hhu\n", a, b);
    return 0;
}

// Output
// Before swap: a=7 b=13
// After swap: a=13 b=7

What kind of magic is this? Well, after those two lines of code: *a ^= *b; *b ^= *a; we can actually say that *b=(*b)^((*a)^(*b)), but because ^ (XOR) is associative and commutative, the relationship also translates to *b=(*b)^(*b)^(*a), which is equivalent to *b=0^(*a), which is equivalent *b=*a, wow, did just b become a?

Again, we can also write *a=((*a)^(*b))^((*b)^((*a)^(*b))), which is equivalent to *a=(*a)^(*a)^(*b), wow, did a just become b ? It looks complicated, but it’s not. Put this on paper, and the mystery will unfold.

Bitwise operations and chars

Characters in C (char) described by this wonderful mapping, more details about ASCII codes here:

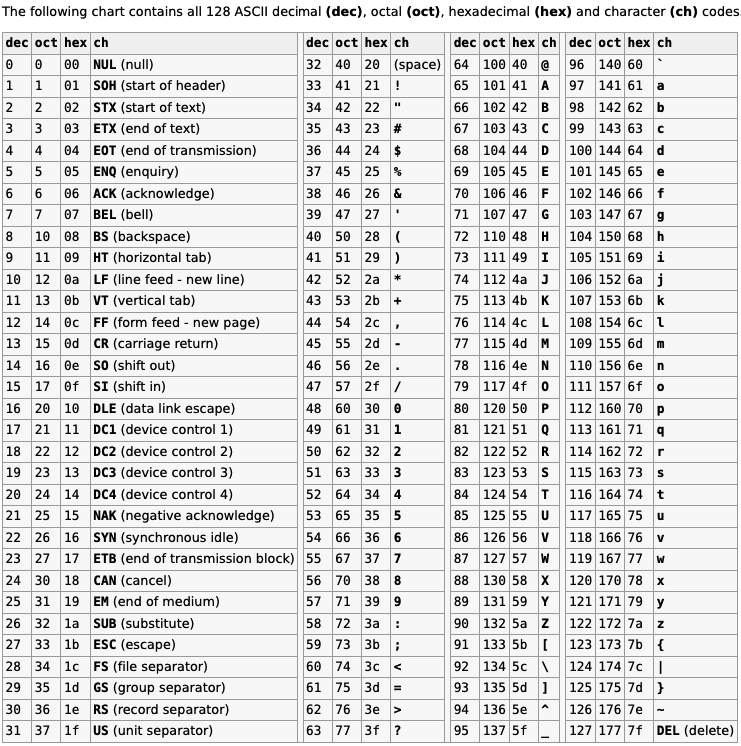
All, without getting deeper into the complicated realm of character encoding, we can undoubtedly say that your average char in C is a number. All the printable char symbols are found in the following interval: [32..126].

The uppercase letters are found inside the interval: [65..90], while the lowercase letters are to be found inside the interval: [61..79]. Because chars are numbers, we can use bitwise operations for them.

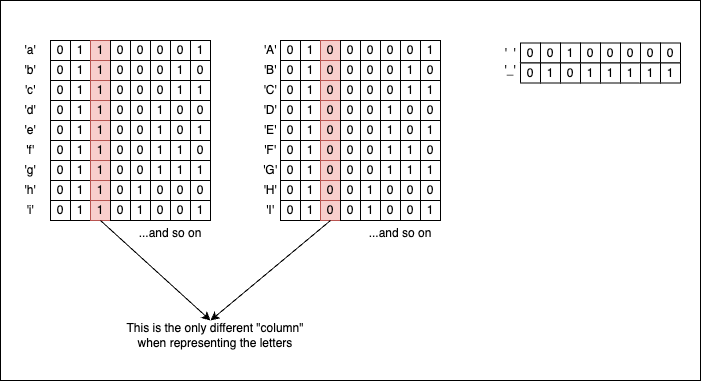
Uppercase and lowercase letters have identical bit patterns, except the column corresponding to 1<<5. So with the right masks put in place, we can transition back and forth from lowercase to uppercase format. But what is the right mask? Well, it’s exactly the one corresponding to 0x20, which is the ' ' (the space) character.

So if we take an uppercase letter and | ' ', we will obtain a lowercase letter because we will activate the bit corresponding to 1<<5.

char *p = "ABCDEFGH";
while(*p) {
    printf("%c", *p | ' ');
    p++;
}
// Output
// abcdefgh

If on the contrary, we take a lowercase letter and & '_' (which corresponds to 0b01011111) we are going to “eliminate” the 1<<5 bit and transform the initial letter to its uppercase form:

char *p = "abcdefgh";
while(*p){
    printf("%c", *p & '_');
    p++;
}

// Ouput
// ABCDEFGH

If we want to toggle the case, we use ^ ' ' (XOR <space>):

char *p = "aBcDeFgH";
while(*p) {
    printf("%c", *p ^ ' ');
    p++;
}
// Output
// AbCdEfG

Other bitwise tricks involving char that you might find interesting are:

// Getting the lowercase letter position in the alphabet
for(char i = 'a'; i <= 'z'; i++) {
    printf("%c --> %d\n", i, (i ^ '`'));
}
// Output
// a --> 1
// b --> 2
// c --> 3
// d --> 4
// e --> 5
// f --> 6
// g --> 7
// ... and so on

// Getting the uppercase letter position in the alphabet
for(char i = 'A'; i <= 'Z'; i++) {
    printf("%c --> %d\n", i, (i & '?'));
}
// Output
// A --> 1
// B --> 2
// C --> 3
// D --> 4
// E --> 5
// F --> 6
// G --> 7
// ... and so on

Gray codes and permutations

Gray Code, also known as Reflected Binary is a binary numeral system where two consecutive numbers differ in only one-bit position. This new way of representing binary numbers is useful in applications such as electronics, where errors due to spurious output transitions can be eliminated using Gray Code instead of the traditional binary code (the one we’ve used until now).

The table of correspondence looks like this:

Decimal	Binary	Gray Code	Decimal Gray
0	0000	0000	0
1	0001	0001	1
2	0010	0011	3
3	0011	0010	2
4	0100	0110	6
5	0101	0111	7
6	0110	0101	5
7	0111	0100	4
8	1000	1100	12
9	1001	1101	13
10	1010	1111	15
11	1011	1110	14
12	1100	1010	10
13	1101	1011	11
14	1110	1001	9
15	1111	1000	8

The algorithm for transitioning from the binary system to the Gray Binary System is as follows:

uint8_t gray_code(uint8_t bv) {
    uint8_t gv = 0;    // 1. We initialize the result with 0
    uint8_t mask = bv; // 2. We use the input binary number as a mask
    while (mask) {     // 3. Until the mask is different than 0
        gv ^= mask;    //       4. We XOR the result with the mask 
        mask >>= 1;    //       5. We shift the mask one bit to the right
    }
    return gv;         // 6. We return the corresponding Gray Code
}

If we run the code, it will return the previously described table of correspondence:

for(uint8_t i = 0; i < 16; i++) {
    print_bits(stdout, i);
    printf(" - ");
    print_bits(stdout, gray_code(i));
    printf("\n");
}

// Output
// 00000000 - 00000000
// 00000001 - 00000001
// 00000010 - 00000011
// 00000011 - 00000010
// 00000100 - 00000111
// 00000101 - 00000110
// 00000110 - 00000100
// ... and so on

A less obvious utilisation of Gray Codes is that we can use them to generate permutations of a given set of elements (such as the characters of string, or the elements of an array). The basic idea is simple, each permutation is a sequence of Gray Codes, where each code represents a swap between adjacent elements. By iterating from all the Gray Codes, we do swaps, and at the same time, generate each permutation.

That’s it

The world of bitwise tricks is much bigger than what was covered in this article. Thank you for reading up until this point. Please check the References section below to see more on the topic.

If you are curious to see some of my code where I did use bitwise operations intensively, please check up the following two articles:

• 4 integers are enough to write a Snake Game
• Writing a simple 16 bit VM in less than 125 lines of C

Around the web

This article has been discussed on:

• lobsters
• hn

References

• Bit Twindling Hacks
• Matters Computational Ideas, Algorithms, Source Code - J¨org Arndt
• What USEFUL bitwise operator code tricks should a developer know about?
• Rounding up to the next power of two in C
• xtrapbits.h