Disclaimer
This article hasn’t been reviewed yet, and it’s still a work in progress.
If you’d like to help out with reviewing, feel free to drop me a message (see the About Page) or leave a comment.
I’ll be gradually adding more problems as time permits (I’m also working on Part 2).
Special thanks to:
meithecatte- for pointing one of the problem statements was incorrect.cryslith- for pointing out some mistakes in my comments and helping me correct a few solutions.- Gheorghe Craciun for inspiring and allowing me to borrow some of his problems.
If I forgot to include a source or mistakenly credited an exercise to the wrong author, please know it was unintentional. Some of the problems are original (created by me), but not all are signed, as the results are too elementary to require attribution. Similarly, some solutions are original, while others are based on official ones—just presented in slightly more detail.
Writing this short article made me nostalgic and brought back fond memories of my high school math teacher, Carmen Georgescu, who had a positive influence on me, as well as Gabriel Tica, who also inspired me when I was a young student.
Introduction
Inequalities are among the most “fascinating” and versatile topics in competitive mathematics because they challenge solvers to think creatively and intuitively. If you look at the IMO problem sets, you will find that inequality problems are almost always present, year after year.
Approaching an “inequality” problem requires more than just sheer “mathematical force” (although using techniques from Real Analysis can help); you need to take a step back and come up with clever manipulations, substitutions, and (sometimes) novel ideas. In essence, inequality problems blend “beauty” with “intellectual challenge”, and they are embodying so well the spirit of “competitive mathematics”.
I am a bad salesperson when it comes to selling mathematics, but the main idea is inequality problems are cool.
- For soccer lovers, solving a hard inequality problem feels like scoring a goal after a long dribbling.
- For video-games lovers, solving a hard inequality problem feels like figuring out a hard puzzle in: Machinarium or The Longest Journey. In the lack of contemporary examples.
- For chess-lovers, solving a hard inequality problem feels like solving a mate-in-six puzzle.
- For competitive programmers, solving a hard inequality feels like solving a hard problem on codeforces.
In case you haven’t seen one, this is what a hard inequality problems look like:
Let \(x_1, x_2, \dots x_n \in \mathbb{R}_{+}\), prove:
\[\sum_{i=1}^n \left[\frac{1}{1+\sum_{j=1}^i x_j}\right] \lt \sqrt{\sum_{i=1}^n \frac{1}{x_i}} \]
Source
The Romanian Math Olympiad, The National Phase.
Let \(a,b,c\) be positive real numbers. Prove that:
\[ \frac{a}{\sqrt{a^2+8bc}} + \frac{b}{\sqrt{b^2+8ac}} + \frac{c}{\sqrt{c^2+8ab}} \ge 1 \].
Source
2001 IMO Problems/Problem 2
It is generally unwise to label something as “hard” or “difficult,” especially in mathematics. However, considering that these problems are actual IMO challenges, it is reasonable to label them in this way.
The purpose of this article is to highlight some techniques and methods that can assist math hobbyists, novice problem solvers, and curious undergraduates in approaching seemingly difficult inequality problems. This writing will only touch upon a small portion of this expansive (debatable epithet) class of problems.
An edgy teacher, names excluded, once said: “In an ideal world people would solve inequality problems instead of Sudoku!”. We haven’t spoken since, I like Sudoku.
Inequations vs. Inequalities
There is a subtle distinction between an inequality and an inequation, although the terms are often used interchangeably in everyday mathematical language.
An inequation, a less common term, behaves just like a mathematical equation involving an inequality symbol. Inequations emphasize the algebraic problem-solving aspect of an inequality.
Those are inequations:
Find real numbers \(x\) for which the following "inequality" holds:
\[ \sqrt{3-x}-\sqrt{x+1} \gt \frac{1}{2} \]
Solution
Solution is left to reader. It's not terribly difficult, even it's an IMO problem. Also there is no "trickonometry" involved.
Source
IMO 1962
An inequation is all about finding solutions, while inequalities focus on the actual relationship between numbers, a statement of truth that applies for all numbers in a given domain.
The following are inequalities:
Problem IVI03 (The modulus inequality)
Let \(a, b\) real numbers. Prove that:
\[ |a+b|\le|a|+|b| \]
Solution
We identify 4 cases:
Both \(a\) and \(b\) are non-negative \((a\ge0, b\ge0)\):
\[|a+b|=a+b=|a|+|b| \]
Both \(a\) and \(b\) are non-positive \((a\le0, b\le0)\):
\[|a+b|=-(a+b)=-a+(-b)=|a|+|b|\]
-
\(a\) and \(b\) have opposite signs. Since the proof is almost identical, we assume \(a\ge0\) and \(b\le0\) and two sub-cases:
- If \(a+b\ge0\) then \(|a+b|=a+b \le a-b = |a|+|b|\).
- If \(a+b\le0\) then \(|a+b|=-a-b \le |a| + |b|\).
The equality holds when \(a\) and \(b\) have the same signs.
Now, let’s try to use the previous result (the modulus inequality) in a creative way:
Let \(a,b\) real numbers. Prove the inequality:
\[ | 1 + ab | + | a + b | \ge \sqrt{|a^2-1||b^2-1|} \]
Hint 1
Consider proving the identity:
\[ \left(a^2-1\right)\left(b^2-1\right) = (1+ab)^2 - (a+b)^2 \]
Hint 2
Consider the previous problem IVI03.
Solution
We begin by using the modulus inequality:
\[ |x| + |y| \geq |x + y|. \]
Applying this to our terms (when \(a+b\) is positive and \(a+b\) is negative), we obtain:
\[ |1+ab| + |a+b| \ge |1+ab+a+b| \] \[ |1+ab| + |a+b| \ge |1+ab-a-b| \]
Multiplying these two inequalities gives:
\[ \left(|1+ab|+|a+b|\right)^2 \geq |1+ab+a+b||1+ab-a-b| \Leftrightarrow \] \[ \left(|1+ab|+|a+b|\right)^2 \geq |(1+ab)^2-(a+b)^2| \Leftrightarrow \] \[ |1+ab|+|a+b| \geq \sqrt{(1+ab)^2-(a+b)^2} \]
Now, let's prove that:
\[ (1+ab)^2-(a+b)^2 = 1 + 2ab + (ab)^2 - a^2 - 2ab - b^2 = \] \[ = a^2(b^2-1)-(b^2-1) = (a^2-1)(b^2-1) \]
Substituting this result back into our inequality::
\[ |1+ab|+|a+b| \ge \sqrt{|a^2-1||b^2-1|} \]
Finally, we analyze the equality case. When does equality hold?
Source
Romanian Math Olympiad, 10th grade, 2008
Let \(x\in\mathbb{R}\). Prove that:
\[ x^2+x+1\gt0 \]
Hint 1
\(a^2\ge0, \forall a\in\mathbb{R}\)
Hint 2
Try multiplying both sides by 2 or completing the square.
Solution 1
We start by multiplying each side by 2:
\[ x^2+x^2+2x+1+1>0 \Leftrightarrow x^2+1+(x+1)^2 > 0 \]
This holds true because \(x^2+1\gt0\) and \((x+1)^2\ge0\).
Solution 2
We rewrite the expression as:
\[ x^2+x+1=x^2+2*x*\frac{1}{2}+(\frac{1}{2})^2+[1-(\frac{1}{2})^2]=(x+\frac{1}{2})^2+\frac{3}{4} \]
Since both terms are non-negative, we conclude that:
\[ (x+\frac{1}{2})^2+\frac{3}{4}>0 \]
Let \(a,b\) real numbers such that \(a+b \gt 0\), prove:
\[ \frac{a^2+b^2}{a+b} \geq \frac{a+b}{2} \]
Solution
We eliminate the denominators using cross-multiplication:
\[ \frac{a^2+b^2}{a+b} \geq \frac{a+b}{2} \Leftrightarrow 2\cdot(a^2+b^2) \geq (a+b)^2 \Leftrightarrow (a-b)^2 \geq 0 \]
The last inequality is always true for real numbers.
Let \(a,b\) real numbers, \(a+b \ge 0\), prove:
\[ \frac{a}{b^2}+\frac{b}{a^2} \ge \frac{1}{a}+\frac{1}{b} \]
Hint 1
\(\frac{1}{a}=\frac{a}{a^2}\)
Solution
We begin by rewriting the given inequality:
\[ \frac{a}{b^2}-\frac{b}{b^2}+\frac{b}{a^2}-\frac{a}{a^2} \ge 0 \]
Rearranging the terms:
\[ \frac{a-b}{b^2}-\frac{a-b}{a^2} \ge 0 \]
Factoring out \(a-b\):
\[ \frac{(a-b)^2*(a+b)}{(ab)^2} \ge 0 \]
Since we know that:
\[ (a-b)^2 \ge 0 , (ab)^2 \ge 0 \text{ and } a+b \ge 0 \]
It follows that:
\[ \Rightarrow \frac{(a-b)^2*(a+b)}{(ab)^2} \ge 0 \]
The equality holds if \(a=b\).
Keep in mind the following two inequalities, as they will be helpful when solving more complex problems:
Let \(x,y,z \in \mathbb{R}\). Prove that:
\[
x^2+y^2+z^2 \ge xy + yz + zx
\]
Try multiplying both sides by 2. Multiplying both sides by 2 and rearranging the terms: \((x-y)^2+(y-z)^2+(z-x)^2 \ge 0\) Since squares of real numbers are always non-negative, the inequality holds. Equality occurs when \(x=y=z\).Hint 1
Solution
Let \(a, b\) be positive real numbers. Prove that:
\[ a^3+b^3 \ge a^2b+ab^2 \]
Solution
Rearranging the given inequality:
\[ a^3+b^3-a^2b-ab^2 \ge 0 \]
Factoring step by step:
\[ a^2(a-b)+b^2(b-a) \ge 0 \Leftrightarrow \\ (a-b)(a^2-b^2) \ge 0 \Leftrightarrow \\ (a-b)(a-b)(a+b) \ge 0 \Leftrightarrow \\ (a-b)^2(a+b) \ge 0 \]
Since \((a-b)^2 \ge 0\) and \(a+b\ge0\), the inequality holds.
Equality occurs when \(a=b\).
For the next problem, consider applying an inequality we have already established.
Let \(a,b,c\) positive real numbers, such that \(abc=1\). Prove the following inequality:
\[ a^4+b^4+c^4 \geq a+b+c \]
Hint 1
\(a^4=\left(a^2\right)^2\)
Solution
We have already established that \(a^2+b^2+c^2\geq ab+bc+ca\). In this regard, let's make use of this fact:
\[ a^4+b^4+c^4 = \left(a^2\right)^2 + \left(b^2\right)^2 + \left(c^2\right)^2 \geq \left(ab\right)^2 + \left(bc\right)^2 + \left(ca\right)^2 \geq \] \[ \geq ab^2c + a^2bc + abc^2 = abc(a+b+c) = abc \]
Equality holds when \(a=b=c\) and \(abc=1\), so \(a=b=c=1\).
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Galati, 2004
In a similar fashion:
Let \(a,b,c\) positive real numbers such that \(abc=1\). Prove the inequality:
\[ \frac{a^3}{bc}+\frac{b^3}{ca}+\frac{c^3}{ab} \geq a+b+c \]
Solution
We start by rewriting the left-hand side over a common denominator:
\[ \frac{a^3}{bc}+\frac{b^3}{ca}+\frac{c^3}{ab} = \frac{a^4+b^4+c^4}{abc} = \] \[ = \frac{(a^2)^2+(b^2)^2+(c^2)^2}{abc} \tag{1} \]
In expression \((1)\), we apply the inequality \(x^2 + y^2 + z^2 \geq xy + yz + zx\) twice (see Problem IVI08), and use the assumption \(abc = 1\):
\[ \frac{(a^2)^2+(b^2)^2+(c^2)^2}{abc} \geq \frac{a^2b^2+b^2c^2+c^2a^2}{abc} \geq \] \[ \geq \frac{abbc+bcca+caab}{abc} = a+b+c \]
Thus, the inequality is proven. Equality holds when \(a = b = c\).
Do you know how to factor your symmetric polynomials ?
For \((x,y)\neq(0,0)\), prove:
\[ x^4+x^3y+x^2y^2+xy^3+y^4\gt0 \]
Hint 1
Did you know about the following identity?
\[ x^n-y^n=(x-y)(x^{n-1}+x^{n-2}y+\dots+xy^{n-2}+y^{n-1}) \]
Solution
Using the identity \(x^n-y^n=(x-y)(x^{n-1}+x^{n-2}y+\dots+xy^{n-2}+y^{n-1}) \), and assuming \(x\neq y\), we can rewrite the given expression as:
\[ x^4+x^3y+x^2y^2+xy^3+y^4 = \frac{x^5-y^5}{x-y} \]
Since \(5\) is an odd number, both \(x^5-y^5\) and \(x-y\) will always have the same sign. This ensures the left-hand side is always positive.
If \(x=y\), the expression simplifies to:
\[x^4+x^3y+x^2y^2+xy^3+y^4=4x^4\]
Thus, the inequality is always true.
I wouldn’t call the next problem a “fundamental” result, but it’s definitely a useful trick that I’ve seen applied to solve at least two or three problems in various math competitions:
Let \(x\) a positive real number such that \(x\gt1\), prove that:
\[ \sqrt{x} \gt \frac{1}{\sqrt{x+1}-\sqrt{x-1}} \]
Solution
To simplify the denominator, multiply by the conjugate expression:
\[ \sqrt{x} \gt \frac{\sqrt{x+1}+\sqrt{x-1}}{(\sqrt{x+1}+\sqrt{x-1})(\sqrt{x+1}-\sqrt{x-1})} \Leftrightarrow \\ \sqrt{x} \gt \frac{\sqrt{x+1}+\sqrt{x-1}}{2} \]
Squaring both sides gives:
\[ x \gt \frac{(\sqrt{x+1}+\sqrt{x-1})^2}{4} = \frac{2x + 2\sqrt{x^2-1}}{4} \]
After simplifying further::
\[ x > \sqrt{x^2-1} \Leftrightarrow x^2 > x^2 - 1. \]
Since \( x > 1 \), the inequality holds true for all \( x > 1 \), completing the proof.
The following two problems have similar solutions. The key idea is to bound each term between two fixed values.
Let \(n \in \mathbb{N}\) and \(n \gt 1\). Prove that:
\[\frac{1}{2}\lt\frac{1}{n+1}+\frac{1}{n+2}+\dots+\frac{1}{2n}\lt\frac{3}{4}\]
Hint 1
\(\frac{1}{n+j}\gt\frac{1}{2n}, \forall j \lt n\)
Solution
To find a lower bound, since each term satisfies \(\frac{1}{n+j} \ge \frac{1}{2n}\), we sum these inequalities:
\[ \frac{1}{n+1}+\frac{1}{n+2}+\dots+\frac{1}{2n}\gt\frac{1}{2n}+\frac{1}{2n}+\dots+\frac{1}{2n}=\frac{1}{2} \]
To find the upper bound, we rewrite the sum in symmetric way:
\[ \frac{1}{n+1}+\frac{1}{n+2}+\dots+\frac{1}{2n}=\frac{1}{2}[(\frac{1}{n}+\frac{1}{2n})+(\frac{1}{n+1}+\frac{1}{2n-1})+\dots] \]
Approximating each term:
\[ \frac{1}{2}[\frac{3n}{2n^2}+\frac{3n}{2n^2+(n-1)}+\dots] < \frac{1}{2}[\frac{3n}{2n^2}+\dots] \]
Summing these fractions:
\[ \frac{3}{4} + \frac{1}{n} < \frac{3}{4} \]
Thus, we have:
\[ \frac{1}{2} \lt \sum_{j=1}^n \frac{1}{n+j} \lt \frac{3}{4} \]
which completes the proof.
Source
This problem is taken from "Culegere de probleme pentru liceu" by Năstăsescu, Niță, Brandiburu, and Joița (1997), a popular mathematics book during my high school years.
Let \(n\in\mathbb{N}^{*}\setminus\{1\}\). Prove that:
\[ \frac{1}{2} \lt \frac{1}{n^2+1} + \frac{2}{n^2+2} + \frac{3}{n^2+3} + \dots + \frac{n}{n^2+n} \lt \frac{1}{2} + \frac{1}{2n} \]
Hint 1
Note that:
\[\frac{1}{n^2+1} \lt \frac{1}{n^2}\]
What can we infer about \(\frac{2}{n^2+2}\)?
Hint 2
On the other hand: \(\frac{1}{n^2+1} \gt \frac{1}{n^2+n}\). What can we deduce about \(\frac{2}{n^2+2}\)?
Solution
First, notice that for each term in the sum, we can replace the denominator with the smaller value to obtain a valid upper bound. Hence, we have:
\[ \frac{1}{n^2+1} + \frac{2}{n^2+2} + \frac{3}{n^2+3} + \dots + \frac{n}{n^2+n} \lt \frac{1}{n^2}+\dots+\frac{n}{n^2} \]
This simplifies to:
\[ \frac{1}{n^2+1} + \frac{2}{n^2+2} + \frac{3}{n^2+3} + \dots + \frac{n}{n^2+n} \lt \frac{1}{n^2}(1+2+\dots+n) = \frac{1}{2}+\frac{1}{2n} \]
Thus, we have the upper bound: \(\frac{1}{2} + \frac{1}{n}\).
Now, we replace each term by its corresponding larger denominator to obtain a lower bound. Specifically, we have:
\[ \frac{1}{n^2+1} + \frac{2}{n^2+2} + \frac{3}{n^2+3} + \dots + \frac{n}{n^2+n} \gt \\ \gt \frac{1}{n^2+n} + \frac{2}{n^2+n} + \dots + \frac{n}{n^2+n} \]
Factoring out \(\frac{1}{n^2+n}\), this simplifies to:
\[ \frac{1}{n^2+1} + \frac{2}{n^2+2} + \frac{3}{n^2+3} + \dots + \frac{n}{n^2+n} \gt \\ \gt \frac{1}{n^2+n}(1+2+\dots+n) = \frac{1}{2} \]
Thus we have a lower bound: \(\frac{1}{2}\).
Combining those results:
\[ \frac{1}{2} \lt \sum_{j=1}^{n} \frac{j}{n^2+j} \lt \frac{1}{2} + \frac{1}{2n} \]
Source
RMO-2002, India
There is something elegant about the next problem:
Prove that for any \(x \in \mathbb{R}_{+}\) the following inequality is true:
\[ \sqrt{x^2+x+\sqrt{x^2+x+\sqrt{x^2+x+\sqrt{x^2+x+\dots+\sqrt{x^2+x}}}}} < x+1 \]
\(n\) is the number of subsequent "radicals".
Hint 1
Try defining the expression recursively after squaring both sides.
Solution
We observe that squaring both sides of the inequality preserves its structure, regardless of the number of nested radicals \(n\):
\[ x^2+x+\sqrt{x^2+x+\sqrt{x^2+x+\sqrt{x^2+x+\dots+\sqrt{x^2+x}}}} < (x+1)^2 \Leftrightarrow \] \[ \sqrt{x^2+x+\sqrt{x^2+x+\sqrt{x^2+x+\dots+\sqrt{x^2+x}}}} < x+1 \]
So, in essence, we need to verify that the base case of the nested radical satisfies the inequality:
\[ \sqrt{x^2+x} < x^2 + 1 \Leftrightarrow x+1 > 0 \]
Since \(x > 0\), the last inequality clearly holds. Therefore, the original inequality is valid.
Source
D.M. Bătineţu-Giurgiu
The following are the first non-trivial challenges in this article that can be solved without using advanced techniques or inequalities. Try using the provided hints before checking the full solution.
Let \(a_1, a_2, \dots, a_n\) positive real numbers such that \(\sum_{i=1}^{2009}a_i = 2009\). Prove the inequality:
\[ \frac{a_1^2+a_2^2}{a_1+a_2}+\frac{a_2^2+a_3^2}{a_2+a_3}+\dots+\frac{a_{2009}^2+a_1^2}{a_{2009}+a_1} \geq 2009 \]
Hint 1
We have already proven the inequality: \[\frac{a^2+b^2}{a+b}\geq\frac{a+b}{2}\]
Solution
From a previous exercise, we know that: \[\frac{a^2+b^2}{a+b}\geq\frac{a+b}{2}\]
Even if we do not remember the exact result, it is natural to try to bound each term individually.
We apply the inequality to each term in the given sum:
\[ \frac{a_1^2+a_2^2}{a_1+a_2}+\frac{a_2^2+a_3^2}{a_2+a_3}+\dots+\frac{a_{2009}^2+a_1^2}{a_{2009}+a_1} \geq \]
Note that each term \( a_i \) appears exactly twice on the right-hand side, and each time with a factor of \( \frac{1}{2} \). Thus, the total becomes:
\[ \frac{a_1+a_2}{2}+\dots+\frac{a_{2009}+a_1}{2} = \sum_{i=1}^{2009}a_i = 2009 \]
Therefore, the inequality is proven.
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Galati, 2009
Let \(a,b,c\) positive real numbers such that: \(abc=1\). Prove that:
\[ \frac{1}{a^3+b^3+1}+\frac{1}{b^3+c^3+1}+\frac{1}{c^3+a^3+1} \leq 1 \]
Hint 1
Try using the inequality \( a^3 + b^3 \geq ab(a + b) \), and use the fact that \( abc = 1 \) to simplify.
Solution
We begin by applying the inequality \( a^3 + b^3 \geq ab(a + b) \). This gives:
\[ \frac{1}{a^3+b^3+1}+\frac{1}{b^3+c^3+1}+\frac{1}{c^3+a^3+1} \leq \] \[ \frac{1}{ab(a+b)+abc}+\frac{1}{bc(b+c)+abc}+\frac{1}{ca(c+a)+abc} = \] \[ \frac{1}{ab(a+b+c)}+\frac{1}{bc(a+b+c)}+\frac{1}{ca(a+b+c)} \]
Now, since \( abc = 1 \), we can substitute \( a = \frac{1}{bc} \), \( b = \frac{1}{ca} \), and \( c = \frac{1}{ab} \), which implies:
\[ \frac{1}{a^3+b^3+1}+\frac{1}{b^3+c^3+1}+\frac{1}{c^3+a^3+1} \leq \] \[ \frac{c}{a+b+c}+\frac{a}{a+b+c}+\frac{b}{a+b+c} = 1 \]
Therefore, the original inequality holds.
Source
Romanian Math Olympiad, Etapa Locala, 8th grade, Galati, 2017
Let \(a,b,c\) positive real numbers such that \(abc=1\). Prove that:
\[ 2\left(\frac{a}{b}+\frac{b}{c}+\frac{a}{a}\right) \geq \frac{1}{a} + \frac{1}{b} + \frac{1}{c} + a + b + c \]
Note
This problem can be approached using more advanced techniques, which will be introduced later in this text. However, it can also be solved using elementary algebraic methods and known inequalities.
Hint 1
Since \( abc = 1 \), try expressing one variable in terms of the others, for example \( c = \frac{1}{ab} \), and reduce the inequality to a two-variable expression.
Hint 2
Recall the inequality:
\[ a^3+b^3 \geq ab(a+b) = ab^2+a^2b \]
Solution
Using the condition \( abc = 1 \), substitute \( c = \frac{1}{ab} \) into the original inequality. The left-hand side becomes:
\[ 2\left(\frac{a}{b} + ab^2 + \frac{1}{a^2b}\right) \geq \frac{1}{a} + \frac{1}{b} + a + b + \frac{1}{ab} \]
We now simplify both sides to a common form. Multiply through as needed to bring all terms to a common denominator. After simplification and rearrangement, the inequality becomes:
\[ 2(a^3+a^3b^3+1)\geq ab+a^2+a^3b^2+a^3b+a^2b^2+a \Leftrightarrow \] \[ (a^3-a^2-a+1)+(a^3b^3-ab-a^2b^2+1)+a^3(b^3-b^2-b+1) \geq 0 \Leftrightarrow \] \[ \underbrace{\left[(a^3+b^3)-a(a+1)\right]}_{\geq 0} + \underbrace{\left[(a^3b^3+1)-ab(ab+1)\right]}_{\geq 0} + \] \[ + \underbrace{a^3\left[(b^3+1)-b(b+1)\right]}_{\geq 0} \geq 0 \]
Now we estimate each group using known inequalities. Recall that:\[a^3 + b^3 \geq ab(a + b)\]
And notice that each grouped expression is of a similar structure, with the general form \( x^3 + y^3 \geq xy(x + y) \). Therefore, each term is non-negative.
Source
Romanian Math Olympiad, Etapa Locala, 8th grade, Galati, 2009
Prove that for each positive integer \(n \gt 1\):
\[ \sqrt{n+1}+\sqrt{n}-\sqrt{2} \gt 1 + \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}} + \dots + \frac{1}{\sqrt{n}} \]
Hint 1
In a previous problem, we proved the following inequality for \( x > 1 \):
\[ \sqrt{x} \gt \frac{1}{\sqrt{x+1}-\sqrt{x-1}} \]
Can you find a way to apply this result to solve the problem?
The idea of using a smaller, known result to prove a more general problem (inequality) is a common and powerful strategy in mathematical problem-solving.
Solution
In a previous exercise, we have already established that:
\[ \sqrt{x} \gt \frac{1}{\sqrt{x+1}-\sqrt{x-1}} \]
Rearranging, this gives:
\[ \sqrt{x+1}-\sqrt{x-1} \gt \frac{1}{\sqrt{x}} \]
Applying this for \( x = 2,3, \dots, n \), we obtain:
\[ \begin{cases} \frac{1}{\sqrt{2}} \lt \sqrt{3}-\sqrt{1} \\ \frac{1}{\sqrt{3}} \lt \sqrt{4}-\sqrt{2} \\ \frac{1}{\sqrt{4}} \lt \sqrt{5}-\sqrt{3} \\ \dots \\ \frac{1}{\sqrt{n}} \lt \sqrt{n+1}-\sqrt{n-1} \end{cases} \]
Summing all these inequalities from \( x = 2 \) to \( x = n \), we get:
\[ (\sqrt{3} - \sqrt{1}) + (\sqrt{4} - \sqrt{2}) + (\sqrt{5} - \sqrt{3}) + \dots + (\sqrt{n+1} - \sqrt{n-1}) > \sum_{i=2}^{n} \frac{1}{\sqrt{i}}. \]
Observing the left-hand side, all intermediate terms cancel, leaving us with:
\[ \sqrt{n+1} + \sqrt{n} - \sqrt{2} -1 > \sum_{i=2}^{n} \frac{1}{\sqrt{i}} \Leftrightarrow \] \[ \sqrt{n+1} + \sqrt{n} - \sqrt{2} > 1 + \sum_{i=2}^{n} \frac{1}{\sqrt{i}}. \]
Thus, the inequality is proven.
Source
Australian Math Olympiad, 1987 (?)
Let \(x,y,z\) positive real numbers. Prove the following inequality:
\[ \frac{1}{x\sqrt{x}+y\sqrt{y}+\sqrt{xyz}} + \frac{1}{y\sqrt{y}+z\sqrt{z}+\sqrt{xyz}}+\frac{1}{z\sqrt{z}+x\sqrt{x}+\sqrt{xyz}} \leq \frac{1}{\sqrt{xyz}} \]
Hint 1
Expressions with radicals often become simpler if you eliminate the roots through substitutions.
Hint 2
Look for a known or previously proven inequality that could simplify the denominators.
Hint 3
You may find the following inequality useful:
\[ a^3+b^3 \geq ab(a+b) \]
Solution
To "remove" the radicals, make the substitutions:
\[ \sqrt{x} \rightarrow a, \quad \sqrt{y} \rightarrow b, \quad \sqrt{z} \rightarrow c \]
The given inequality becomes:
\[ \begin{align} \frac{1}{a^3+b^3+abc}+\frac{1}{b^3+c^3+abc}+\frac{1}{c^3+a^3+abc} \leq \frac{1}{abc} \tag{1} \end{align} \]
From a prior problem (or a standard inequality):
\[ \begin{align} a^3+b^3 \geq ab(a+b) \Leftrightarrow (a-b)^2(a+b) \geq 0 \tag{2} \end{align} \]
Applying \((2)\) for each denominator in \((1)\):
\[ \frac{1}{a^3+b^3+abc}+\frac{1}{b^3+c^3+abc}+\frac{1}{c^3+a^3+abc} \leq \] \[ \leq \frac{1}{ab(a+b)+abc}+\frac{1}{bc(b+c)+abc}+\frac{1}{ca(c+a)+abc} = \] \[ = \frac{1}{ab(a+b+c)}+\frac{1}{bc(a+b+c)}+\frac{1}{ca(a+b+c)} = \] \[ = \frac{c}{abc(a+b+c)}+\frac{a}{abc(a+b+c)} + \frac{b}{abc(a+b+c)} = \] \[ = \frac{(a+b+c)}{(a+b+c)abc} = \frac{1}{abc} \]
Thus we obtain the desired inequality.
Equality holds when \(a=b=c\), or when \(x=y=z\).
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Timis, 2013
Let \(a,b,c\) positive real numbers such that \(ab+bc+ca=1\). Prove the inequality:
\[ \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a} \ge \sqrt{3} + \frac{ab}{a+b} + \frac{bc}{b+c} + \frac{ca}{c+a} \]
Hint 1
Rearrange the inequality so that all terms involving \(a, b,\) and \(c\) are on the left-hand side.
Hint 2
Use the given condition \(ab+bc+ca=1\) to rewrite the expressions \(1 - ab\), \(1 - bc\), and \(1 - ca\) in terms of \(a, b,\) and \(c\).
Solution
Rewriting the given inequality by moving all terms involving \(a, b,\) and \(c\) to the left-hand side, we obtain:
\[ \frac{1 - ab}{a+b}+\frac{1 - bc}{b+c}+\frac{1 - ca}{c+a} \geq \sqrt{3}. \]
Since \(ab+bc+ca=1\), we use the following identities:
\[ 1 - ab = bc + ca, \quad 1 - bc = ab + ca, \quad 1 - ca = ab + bc. \]
Substituting these into the inequality, we get:
\[ \frac{bc+ca}{a+b} + \frac{ab+ca}{b+c} + \frac{ab+bc}{c+a} \geq \sqrt{3}. \]
Rewriting each fraction:
\[ \frac{a(b+c)}{b+c} + \frac{b(c+a)}{c+a} + \frac{c(a+b)}{a+b} \geq \sqrt{3}. \]
Since each term simplifies we conclude:
\[ a + b + c \overbrace{\geq}^{?} \sqrt{3}. \]
Squaring both sides, we obtain:
\[ (a + b + c)^2 \geq 3. \]
Expanding the left-hand side:
\[ a^2 + b^2 + c^2 + 2(ab + bc + ca) \geq 3. \]
Since \(ab + bc + ca = 1\), substituting this yields:
\[ a^2 + b^2 + c^2 + 2 \geq 3. \]
Finally, using the well-known inequality \(a^2 + b^2 + c^2 \geq ab + bc + ca = 1\), we add \(2\) to both sides:
\[ a^2 + b^2 + c^2 + 2 \geq 3. \]
This confirms the inequality.
Source
Romanian Math Olympiad, 9th grade, 2002
Let \(a,b,c\) positive real numbers such that \(a+b+c\le4\) and \(ab+bc+ca\ge4\). Prove that at least two of the following inequalities must hold at all times:
\[ \begin{cases} |a-b| \le 2\\ |b-c| \le 2\\ |c-a| \le 2 \end{cases} \]
Hint 1
Try expanding \((a+b+c)^2\)
Hint 2
Starting with \( (a+b+c)^2 \le 16 \), can you derive the alternate form: \( (a-b)^2 + (b-c)^2 + (c-a)^2 \le 8 \)
Solution
Since \(a+b+c\le4\) we have \((a+b+c)^2 \le 16\).
Expanding \((a+b+c)^2\) gives:
\[ (a+b+c)^2 \le 16 \Leftrightarrow \\ a^2+b^2+c^2 + 2(ab+bc+ca) \le 16 \Leftrightarrow \\ a^2+b^2+c^2 \le 8 \Leftrightarrow \\ a^2+b^2+c^2 - ab - bc - ca \le 4 \Leftrightarrow \\ a^2 - 2ab + b^2 + b^2 - 2bc + c^2 + c^2 - 2ca + a^2 \le 8 \Leftrightarrow \\ (a-b)^2 + (b-c)^2 + (c-a)^2 \le 8 \]
Now, suppose \(|a-b| \le 2\) and \(|b-c| \le 2\) are false. This would mean that \( |a - b| > 2 \) and \( |b - c| > 2 \), which leads to a contradiction.
Source
This problem is adapted from the book: T. Andreescu, Z. Feng - 101 Problems in Algebra (Korean Mathematics Competition, 2001).
Weak Inequalities vs. Strict inequalities
Weak inequalities are inequalities that allow for the possibility of equality. . They are typically denoted by the symbols \(\ge\) or \(\le\). In contrast, strict inequalities, use \(\gt\) and \(\lt\) and they don’t permit equality.
A renaissance way to grasp the concept of a weak inequality is to think of the “finger of God” touching Adam’s hand. In this metaphor, a strict inequality is represented by the following painting, as it depicts a situation that never occurs — at least not in olam ha-ze (this world).

From a mathematical standpoint, we know, for example, that \(x^2+y^2\ge2xy\). This inequality is always true because \((x-y)^2\ge0\). If we plot \(x^2+y^2\), and \(2xy\), we will a see thin line where the graphical representation “touch”. This red line is key to solving many problems in physics and engineering. It is specific to weak inequalities.
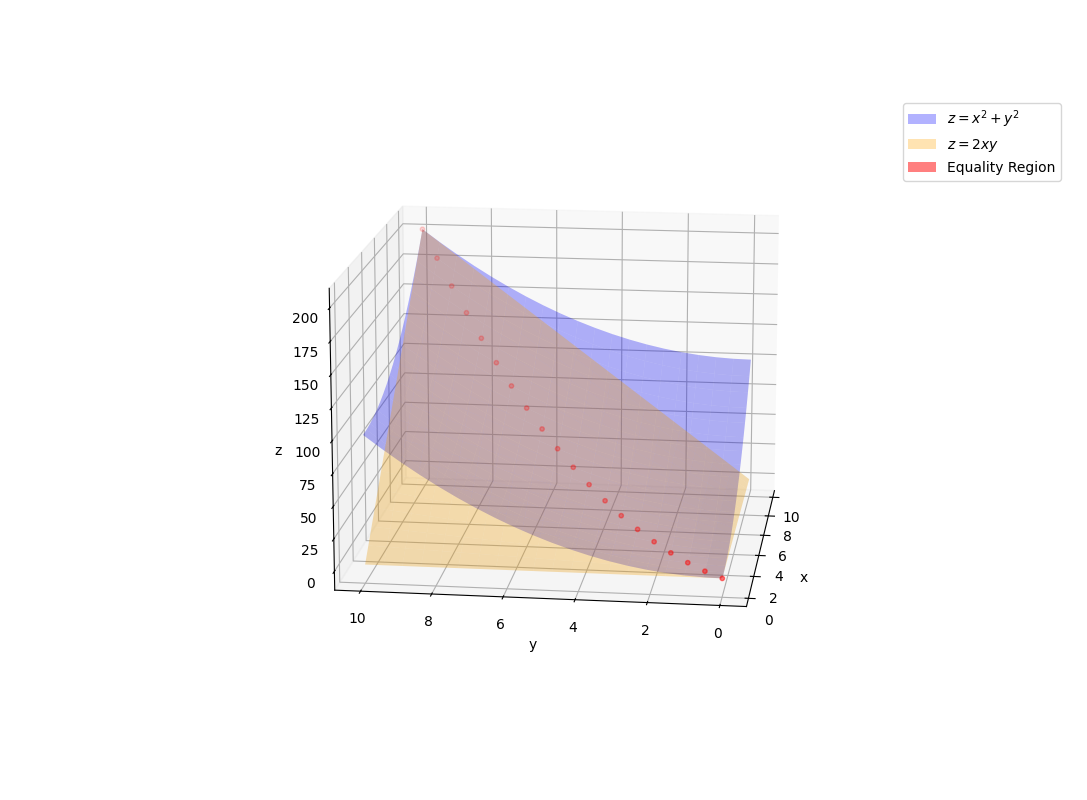
All in all, the main idea is that weak inequalities are more interesting than strict inequalities.
Being playful with algebraic identities
Before delving into specific inequalities, it’s important to highlight a few key identities that problem creators frequently use when designing challenges. These identities are not only essential for understanding inequalities but also serve as powerful tools for solving a variety of other problems.
Some of my favorite identities are:
- \(\hspace{1cm} 2(x^2+y^2)=(x+y)^2+(x-y)^2 \)
- \(\hspace{1cm} x^3+y^3=(x+y)(x^2-xy+y^2) \)
- \(\hspace{1cm} x^3-y^3=(x-y)(x^2+xy+y^2) \)
- \(\hspace{1cm} x^n-y^n=(x-y)(x^{n-1}+x^{n-2}y+\dots+xy^{n-1}+y^n) \)
- \(\hspace{1cm} 2(xy+yz+zx)=(x+y+z)^2-(x^2+y^2+z^2) \)
- \(\hspace{1cm} 3(x+y)(y+z)(z+x)=(x+y+z)^3-(x^3+y^3+z^3) \)
- \(\hspace{1cm} (x+y)(y+z)(z+x)=(x+y+z)(xy+yz+zx)-xyz \)
- \(\hspace{1cm} x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx) \)
- \(\hspace{1cm} (\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}})^2 = (a+b)(\frac{1}{a}+\frac{1}{b})\)
- \(\hspace{1cm} \frac{x}{(x-y)(x-z)}+\frac{y}{(y-x)(y-z)}+\frac{z}{(z-x)(z-y)}=0 \)
- \(\hspace{1cm} \frac{x^2}{(x-y)(x-z)}+\frac{y^2}{(y-x)(y-z)}+\frac{z^2}{(z-x)(z-y)}=1 \)
- \(\hspace{1cm} \frac{x^3}{(x-y)(x-z)}+\frac{y^3}{(y-x)(y-z)}+\frac{z^3}{(z-x)(z-y)}=x+y+z \)
Should you memorize all of these identities? It depends. If you’re actively participating in contests, I believe it’s worth memorizing them. Otherwise, simply being aware of their existence is sufficient. When you come across similar structures, check if these identities can help you. In a contest, you can present them as lemmas, and for clarity, it’s advisable to offer brief proofs. Fortunately, the proofs are typically straightforward, relying on simple algebraic manipulations.
For example, consider the following problems:
Let \(x,y,z \in \mathbb{R}^{*}\), where \(x< y < z\), and \(\frac{x^2}{yz}+\frac{y^2}{xz}+\frac{z^2}{xy}=3\). Prove that the arithmetic mean of \(x,y,z\) is 0.
Hint 1
Multiply both sides with \(xyz\).
Hint 2
Use the identity:
\(x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)\)
Solution
The arithmetic mean of \(x,y,z\) is \(\frac{x+y+z}{3}=0\). Thus, we will need to prove that \(x + y + z = 0\).
Multiplying both sides by \(xyz\), the given expression becomes:
\[x^3+y^3+z^3-3xyz=0\]
Using the identity from Hint 2, we can conclude that:
\[0=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)\]
This implies one of the following two cases: \[ \begin{cases} x+y+z=0 \text{ or} \\ x^2+y^2+z^2-xy-yz-zx=0 \\ \end{cases} \]
Now, let's consider the second case:
\[ x^2+y^2+z^2-xy-yz-zx=0 \Leftrightarrow \\ 2x^2+2y^2+2z^2-2xy-2yz-2zx=0 \Leftrightarrow \\ x^2-2xy+y^2+y^2-2yz+z^2+z^2-2zx+x^2=0 \Leftrightarrow \\ (x-y)^2+(y-z)^2+(z-x)^2=0 \]
This implies that \((x-y)=0\), \((y-z)=0\) and \((z-x)=0\) leading to \(x = y = z\).
However, this contradicts the assumption that \(x < y < z\). Therefore, the only valid conclusion is that \(x + y + z = 0\).
Source
Andrei N. Ciobanu
Find all pairs of distinct non-negative natural numbers \((x,y)\) such that:
\[x^3+y^3=(x+y)^2\]
Hint 1
Look for a suitable identity that can help simplify the expression.
Hint 2
Use the identity:
\[x^3+y^3=(x+y)(x^2-xy+y^2)\]
Solution
Using the identity \(x^3 + y^3 = (x + y)(x^2 - xy + y^2)\), we can rewrite the equation as:
\[x+y=x^2-xy+y^2\]
Next, we rearrange the terms to form a quadratic equation in \(x\):
\[ x^2-(y+1)x+(y^2-y)=0 \]
Now, we compute the discriminant, \(\Delta\), under the condition that \(\Delta \geq 0\):
\[ \Delta = -3y^2+6y+1 \geq 0 \]
This inequality simplifies to:
\[ \frac{3-2\sqrt{3}}{3} \le y \le \frac{3+2\sqrt{3}}{3} \]
The possible values of \(y\) that satisfy this condition are \(y = 1, 2\). Substituting these values back into the equation gives the pairs of solutions:
\[ (x, y) = (1, 0), (0, 1), (1, 2), (2, 1), (2, 2). \]
Source
This problem was sourced and adapted from the book: T. Andreescu, Z. Feng - 101 Problems in Algebra
This wasn’t an inequality problem, but similar structures can arise in various contexts. Knowing your identities can significantly reduce the effort required to solve a problem.
If you enjoyed the previous problem, give the next one a try:
Let \(x,y,z \in \mathbb{R}\), and assume that \((x+y+z)^3=x^3+y^3+z^3\). Prove that for all \(n \in \mathbb{N}\), the following holds:
\[(x+y+z)^{2n+1}=x^{2n+1}+y^{2n+1}+z^{2n+1}\]
Hint 1
Can you identify and use an identity that connects \((x + y + z)^3\) with \(x^3 + y^3 + z^3\)?
Hint 2
Use the fact that \( (x + y + z)^3 - (x^3 + y^3 + z^3) = 3(x + y)(y + z)(z + x) \).
Solution
No solution has been provided here. If you'd like, you can email me for a solution.
Source
This problem was sourced from "Culegere de probleme pentru liceu," by Nastasescu, Nita, Brandiburu, and Joita, 1997, a popular math book during my high school years.
The AM-GM Inequality
The AM (Arithmetic Mean) - GM (Geometric Mean) is a fundamental result in algebra that states:
For any set of non-negative real numbers \(a_1, a_2, \dots , a_n\) the arithmetic mean is always greater than or equal to the geometric mean:
\[ \frac{a_1+a_2+\dots+a_n}{n} \ge \sqrt[n]{a_1*a_2*\dots*a_n} \]
Or:
\[ \sum_{i=1}^n a_i \ge n \sqrt[n]{\prod_{i=1}^n a_i} \]
The equality holds, if, and only if \(a_1=a_2=\dots=a_n\).
For \(n=2\) the inequality can be written as: \(\frac{a+b}{2} \ge \sqrt{ab}\).
For \(n=3\) the inequality can be written as: \(\frac{a+b+c}{3} \ge \sqrt[3]{abc}\).
An interesting case arises when \(\prod_{i=1}^na_i=1\). In this situation, the inequality gives us: \(\sum_{i=1}a_i \ge n\), which means the sum of the numbers is always greater than or equal to \(n\) (the number of numbers).
With that in mind, let’s move on to the following problems:
Let \(x \in \mathbb{R}_{+}\) prove that:
\[x+\frac{1}{x} \ge 2\]
Solution
To prove the inequality, we apply the Arithmetic Mean - Geometric Mean (AM-GM) inequality to the numbers \(x\) and \(\frac{1}{x}\)::
\[ \frac{x+\frac{1}{x}}{2} \ge \sqrt{x*\frac{1}{x}} \Leftrightarrow x + \frac{1}{x} \ge 2 \]
Equality holds when \(x = \frac{1}{x}\), which implies \(x = 1\).
Now, let’s extend this concept by solving the following problem:
Let \(x_1,x_2,\dots,x_n \in \mathbb{R}_{+}\). Prove that:
\[S=\frac{x_1}{x_2}+\frac{x_2}{x_3}+\dots+\frac{x_{n-1}}{x_n}+\frac{x_n}{x_1} \ge n \]
Hint 1
What happens if you multiply each term in the sum?
Solution
To prove the inequality, we apply the AM-GM Inequality:
\[ \frac{S}{n} \ge \sqrt[n]{\frac{x_1}{x_2}\frac{x_2}{x_3}\dots\frac{x_n}{x_1}} \Leftrightarrow S \ge n*\sqrt[n]{1} \Leftrightarrow S \ge n \]
Equality holds if \(x_1 = x_2 = \dots = x_n\).
With a bit of creativity, you can solve the next problem in a manner similar to the previous one.
Let \(n\) be a positive integer greater than \(1\). Show that:
\[ \frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}+\dots+\frac{1}{2n-1} \gt n \left(\sqrt[n]{2} - 1\right) \]
Hint 1
The inequality can be rewritten in an equivalent form:
\[ \frac{1}{n}\left(n+\frac{1}{n}+\frac{1}{n+1}+\dots+\frac{1}{2n-1}\right) \gt \sqrt[n]{2} \]
Hint 2
Consider splitting \(n\) as a sum of ones:
\[ \frac{1}{n}\left(\underbrace{1+1+\dots+1}_{n}+\frac{1}{n}+\frac{1}{n+1}+\dots+\frac{1}{2n-1}\right) \gt \sqrt[n]{2} \]
Solution
We start by rewriting the given inequality::
\[ \frac{1}{n}+\frac{1}{n+1}+\dots+\frac{1}{2n-1} \gt n \left(\sqrt[n]{2} - 1\right) \Leftrightarrow \\ \]
Which is equivalent to:
\[ \frac{1}{n}\left(n+\frac{1}{n}+\frac{1}{n+1}+\dots+\frac{1}{2n-1}\right) \gt \sqrt[n]{2} \]
Now, split \(n\) into a sum of ones and distribute them across the terms inside the parentheses:
\[ \frac{1}{n}*\left[\left(1+\frac{1}{n}\right)+\left(1+\frac{1}{n+1}\right) + \dots + \left(1+\frac{1}{2n-1}\right)\right] \gt \sqrt[n]{2} \Leftrightarrow \\ \frac{1}{n}*\left( \frac{n+1}{n} + \frac{n+2}{n+1} + \dots + \frac{2n}{2n-1} \right) \overbrace{\gt}^{AM-GM} \sqrt[n]{\frac{n+1}{n}*\dots*\frac{2n}{2n-1}} \gt \sqrt[n]{2} \]
This proves our inequality. Equality would hold for \(n=1\), which is not possible given the constraints.
Source
Australian Math Olympiad, 1992
Do you know your Partial fraction decomposition ?
Prove that \(\forall n \in [5,\infty) \cap \mathbb{N}\):
\[ \frac{1}{1*3}+\frac{1}{3*5}+\dots+\frac{1}{(n-2)n}\gt\frac{1}{\sqrt{n}}-\frac{1}{n} \]
Hint 1
Did you know that you can express the following sum as:
\[ \frac{1}{1*2}+\frac{1}{2*3}+\frac{1}{3*4}+\dots+\frac{1}{(n-1)n} = \\ = \frac{2-1}{1*2}+\frac{3-2}{2*3}+\dots+\frac{n-(n-1)}{(n-1)n} = \\ = \frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\dots-\frac{1}{n}=1-\frac{1}{n} \]
Hint 2
How can we use the relationship from Hint 1 to our advantage?
Solution
We start by manipulating the sum:
\[ \frac{1}{1*3}+\frac{1}{3*5}+\dots+\frac{1}{(n-2)n} \gt \frac{1}{\sqrt{n}}-\frac{1}{n} \]
This simplifies to:
\[ \frac{1}{2}\Bigl[\frac{3-1}{1*3}+\frac{5-3}{3*5}+\dots+\frac{n-(n-2)}{(n-2)n}\Bigl] \gt \frac{1}{\sqrt{n}}-\frac{1}{n} \Leftrightarrow \\ \frac{1}{2}\Bigl(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\dots-\frac{1}{n}\Bigl) \gt \frac{1}{\sqrt{n}}-\frac{1}{n} \Leftrightarrow \\ \frac{1}{2}-\frac{1}{2n}+\frac{1}{n} \gt \frac{1}{\sqrt{n}} \]
We then obtain:
\[ \frac{1}{2}+\frac{1}{2n} \gt \frac{1}{\sqrt{n}} \Leftrightarrow \\ \frac{1+\frac{1}{n}}{2} \gt \sqrt{1*\frac{1}{n}} \]
The equality holds only when \(n = 1\), but this is not an acceptable value for \(n\).
What if you apply the AM-GM inequality twice?
Let \(a,b\) positive real numbers, prove:
\[ a^4+b^4 \geq 2\sqrt{2}ab^2-1 \]
Solution
To solve this problem we need to apply the AM-GM inequality twice, in the following manner:
\[ (a^4+1)+b^4 \overbrace{\geq}^{\text{AM-GM}} 2a^2+b^4 \overbrace{\geq}^{\text{AM-GM}} 2b^2a\sqrt{2} \]
The AM-GM inequality reveals a profound connection between the sum (∑) and the product (∏) of positive real numbers. With this insight in mind, let’s explore and solve the following problems:
Let \(x_1, x_2, \dots x_n\) be non-negative and positive real numbers. Can you find a value for \(P=\prod_{i=1}^nx_i\) so that \(S=\sum_{i=1}^n x_i \ge \pi\) ?
Solution
We wish to find a value for \(P\) such that the inequality \(S\ge\pi\) holds.
Consider the following choice for \(P\):
\[ P=\prod_{i=1}^n x_i = (\frac{\pi}{n})^n \]
Now, applying the Arithmetic Mean-Geometric Mean (AM-GM) inequality, we have:
\[ \sum_{i=1}^n x_i \ge n \sqrt[n]{(\frac{\pi}{n})^n} = \pi \]
Q.E.D.
Let \(x,y,a,b \gt 0\), prove that:
\[ \frac{a}{x}+\frac{b}{y} \ge \frac{4(ay+bx)}{(x+y)^2} \]
Solution
We begin by simplifying the left-hand side:
\[ \frac{a}{x}+\frac{b}{y}=\frac{ay+bx}{xy} \]
Thus, the inequality becomes:
\[ \frac{ay+bx}{xy} \ge \frac{4(ay+bx)}{(x+y)^2} \Leftrightarrow \frac{1}{xy} \ge \frac{4}{(x+y)^2} \Leftrightarrow \Bigl(\frac{x+y}{2}\Bigl)^2 \ge xy \]
This is a well-known result from the Arithmetic Mean-Geometric Mean (AM-GM) inequality, which states that:
\[ \Bigl(\frac{x+y}{2}\Bigl)^2 \ge xy \]
Thus, the original inequality holds, with equality if and only if \(x=y\).
Source
The Romanian Math Olympiad
Now, for a bit of fun, let’s tackle a problem that may appear more challenging at first glance. You just need to apply the AM-GM twice.
Let \(a,b,c\) positive real numbers. Prove that:
\[ \frac{1}{x^2+yz}+\frac{1}{y^2+zx}+\frac{1}{z^2+xy} \leq \frac{1}{2}\left(\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}\right) \]
Hint 1
Can you apply the AM-GM inequality to the denominator?
Hint 2
Using the AM-GM inequality, observe that:
\[ \frac{1}{\underbrace{x^2+yz}_{\ge 2x\sqrt{xy}}} \le \frac{1}{2x\sqrt{xy}} = \frac{\sqrt{xy}}{2xyz} \]
Apply this result to each term in the sum.
Solution
Applying the AM-GM inequality to each denominator, we obtain:
\[ x^2 + yz \geq 2x\sqrt{yz}, \quad y^2 + zx \geq 2y\sqrt{zx}, \quad z^2 + xy \geq 2z\sqrt{xy}. \]
Taking reciprocals and using the fact that if \(a \geq b > 0\), then \(\frac{1}{a} \leq \frac{1}{b}\), we get:
\[ \frac{1}{x^2+yz} \leq \frac{1}{2x\sqrt{yz}}, \quad \frac{1}{y^2+zx} \leq \frac{1}{2y\sqrt{zx}}, \quad \frac{1}{z^2+xy} \leq \frac{1}{2z\sqrt{xy}}. \]
Summing these inequalities, we obtain:
\[ \frac{1}{x^2+yz} + \frac{1}{y^2+zx} + \frac{1}{z^2+xy} \leq \frac{1}{2} \left( \frac{\sqrt{yz}}{xyz} + \frac{\sqrt{zx}}{xyz} + \frac{\sqrt{xy}}{xyz} \right). \]
Applying the AM-GM inequality again, we observe that:
\[ \sqrt{yz} + \sqrt{zx} + \sqrt{xy} \leq \frac{(x+y) + (y+z) + (z+x)}{2} = x+y+z. \]
Thus, we obtain:
\[ \frac{1}{x^2+yz}+\frac{1}{y^2+zx}+\frac{1}{z^2+xy} \leq \frac{1}{2xyz} (x + y + z). \]
Rewriting the right-hand side in terms of fractions, we get:
\[ \frac{1}{2xyz} (x+y+z) = \frac{1}{2} \left( \frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx} \right). \]
Thus, the desired inequality holds. Equality occurs when \( x = y = z \).
Source
Romanian Math Olympiad, 2006
The following problem was shortlisted for the 1971 International Mathematical Olympiad. While not particularly difficult, it requires discovering a clever trick.
Let \(a_1, a_2, a_3, a_4\) be positive real numbers. Prove the the inequality:
\[ \frac{a_1+a_3}{a_1+a_2} + \frac{a_2+a_4}{a_2+a_3} + \frac{a_3+a_1}{a_3+a_4} + \frac{a_4+a_2}{a_4+a_1} \ge 4 \]
Hint 1
A direct consequence of the AM-GM inequality is:
\[ (a+b)^2 \ge 4ab \]
Hint 2
Applying the result from "Hint 1" gives:
\[ 4(a_1+a_2)(a_3+a_4) \leq (a_1+a_2+a_3+a_4)^2 \Leftrightarrow \\ \Leftrightarrow \frac{1}{(a_1+a_2)(a_3+a_4)} \geq \frac{4}{(a_1+a_2+a_3+a_4)^2} \]
Solution
To bring the fractions to a common denominator, rewrite the given sum as:
\[ E = \frac{a_1+a_3}{a_1+a_2} + \frac{a_2+a_4}{a_2+a_3} + \frac{a_3+a_1}{a_3+a_4} + \frac{a_4+a_2}{a_4+a_1} = \\ \frac{a_1+a_3}{a_1+a_2} + \frac{a_3+a_1}{a_3+a_4} + \frac{a_2+a_4}{a_2+a_3} + \frac{a_4+a_2}{a_4+a_1} = \\ \frac{(a_1+a_3)(a_1+a_2+a_3+a_4)}{(a_1+a_2)(a_3+a_4)} + \frac{(a_2+a_4)(a_1+a_2+a_3+a_4)}{(a_4+a_1)(a_2+a_3)} \]
Using the AM-GM inequality (see Hint 1 and Hint 2):
\[ \begin{cases} \frac{1}{(a_1+a_2)(a_3+a_4)} \ge \frac{4}{(a_1+a_2+a_3+a_4)^2} \\ \frac{1}{(a_1+a_4)(a_2+a_3)} \ge \frac{4}{(a_1+a_2+a_3+a_4)^2} \end{cases} \]
Substituting these bounds into the expression for \(E\):
\[ E \ge \frac{4(a_1+a_3)(a_1+a_2+a_3+a_4)}{(a_1+a_2+a_3+a_4)^2} + \frac{4(a_2+a_4)(a_1+a_2+a_3+a_4)}{(a_1+a_2+a_3+a_4)^2} = \\ = \frac{4(a_1+a_3)}{a_1+a_2+a_3+a_4} + \frac{4(a_2+a_4)}{a_1+a_2+a_3+a_4} = \frac{4(a_1+a_2+a_3+a_4)}{a_1+a_2+a_3+a_4} = 4 \]
Thus, the inequality is proven.
When does the equality hold?
Source
IMO 1971, Short List
For the next exercise the key idea is to leverage the additional conditions provided and incorporate them into your proof of the main inequality.
Let \(a,b,c\) positive real numbers such that \(abc=1\). Prove that:
\[ \frac{c+ab+1}{1+a+a^2}+\frac{a+bc+1}{1+b+b^2}+\frac{b+ca+1}{1+c+c^2} \ge 3 \]
Hint 1
Since \(abc=1\), we can rewrite the terms as:
\[ \frac{c+ab+1}{1+a+a^2}=\frac{abc^2+ab+abc}{1+a+a^2} \]
Solution
Given \(abc=1\) we can express the sum as:
\[ \frac{c+ab+1}{1+a+a^2}+\frac{a+bc+1}{1+b+b^2}+\frac{b+ca+1}{1+c+c^2} = \] \[ = \frac{abc^2+ab+abc}{1+a+a^2}+\frac{a^2bc+bc+abc}{1+b+b^2}+\frac{ab^2c+ca+abc}{1+c+c^2} = \] \[ = ab(\frac{1+c+c^2}{1+a+a^2})+bc(\frac{1+a+a^2}{1+b+b^2})+ca(\frac{1+b+b^2}{1+c+c^2}) \]
By the Arithmetic Mean-Geometric Mean (AM-GM) inequality, we have:
\[ ab(\frac{1+c+c^2}{1+a+a^2})+bc(\frac{1+a+a^2}{1+b+b^2})+ca(\frac{1+b+b^2}{1+c+c^2}) \overbrace{\ge}^{AM-GM} 3\sqrt{a^2b^2c^2} = 3 \]
Equality holds when \(a=b=c=1\).
Sometimes you can solve “inequations” using “inequalities”:
Find \(x,y,z \in [\frac{1}{3}, \infty)\) such that \(x+y+z \leq 4\) and \(\sqrt{3x-1}+\sqrt{3y-1}+\sqrt{3z-1} \geq 3\sqrt{3}\).
Hint 1
Notice that the second inequality can be rewritten as:
\[ \sqrt{x-\frac{1}{3}}+\sqrt{x-\frac{1}{3}}+\sqrt{x-\frac{1}{3}} \geq 3 \]
Solution
The key intuition for problems like this is to "trap" the value of the given sum between constants to force equality. Specifically, we aim to find a real number \(k\) such that:
\[ k \leq \sqrt{3x-1}+\sqrt{3y-1}+\sqrt{3z-1} \leq k \]
Once we achieve this, we can determine the values of \(x, y, z\) by analyzing the equality conditions.
Then we can "force" the equality conditions and find the numbers.
First, notice that the second inequality transforms as follows:
\[ \sqrt{3x-1}+\sqrt{3y-1}+\sqrt{3z-1} \geq 3\sqrt{3} \Leftrightarrow \] \[ \Leftrightarrow \sqrt{x-\frac{1}{3}} + \sqrt{y-\frac{1}{3}} + \sqrt{z-\frac{1}{3}} \geq 3 \tag{1} \]
Now, we can apply the AM-GM inequality (Arithmetic Mean-Geometric Mean Inequality) in a "forced" way. Remember that for each positive number \(a\), \(\sqrt{a} \leq \frac{a+1}{2}\) Applying this to each term separately, we get:
\[ \sqrt{x-\frac{1}{3}} \leq \frac{x-\frac{1}{3}+1}{2} = \frac{3x+2}{6} \tag{2} \] \[ \sqrt{y-\frac{1}{3}} \leq \frac{y-\frac{1}{3}+1}{2} = \frac{3y+2}{6} \tag{3} \] \[ \sqrt{z-\frac{1}{3}} \leq \frac{z-\frac{1}{3}+1}{2} = \frac{3z+2}{6} \tag{4} \]
Adding inequalities \((2)\), \((3)\), (\(4\)) and using the condition \(x+y+z \leq 4\), we further obtain:
\[ \sqrt{x-\frac{1}{3}} + \sqrt{y-\frac{1}{3}} + \sqrt{z-\frac{1}{3}} \leq \frac{3(\overbrace{x+y+z}^{\leq 4})+6}{6} \leq 3 \tag{5} \]
From \((1)\) and \((5)\), it follows that:
\[ 3 \leq \sqrt{x-\frac{1}{3}} + \sqrt{y-\frac{1}{3}} + \sqrt{z-\frac{1}{3}} \leq 3 \]
Thus, equality must occur throughout. In particular, equality must hold when applying AM-GM, meaning that:
\[ x-\frac{1}{3} = 1 \Rightarrow x=\frac{4}{3} \] \[ y-\frac{1}{3} = 1 \Rightarrow y=\frac{4}{3} \] \[ z-\frac{1}{3} = 1 \Rightarrow z=\frac{4}{3} \]
Therefore, the only solution is \(x = y = z = \frac{4}{3}\).
Source
Gheorghe F. Molea
Cyclic and Symmetrical Inequalities
Before proceeding further, let’s familiarize ourselves with two important notions: cyclic inequalities and symmetrical inequalities.
A cyclic inequality involves a set of variables arranged in a cyclic order, where each term follows a repeating pattern by “rotating” the variables. For instance, for three variables we perform the transformation:
\[ a \rightarrow b, \quad b \rightarrow c, \quad c \rightarrow a \]
The cyclic behavior can be expressed using the notation:
\[ \sum_{\text{cyc}} f(a,b,c) = f(a,b,c) + f(b,c,a) + f(c,a,b) \]
Here are some examples that illustrate cyclic sums and their corresponding inequalities:
\[ \sum_{\text{cyc}} a^2 = a^2+b^2+c^2 \overbrace{\geq}^{AM-GM} 3\sqrt[3]{(abc)^2} \] \[ \sum_{\text{cyc}} \frac{a}{b} = \frac{a}{b} + \frac{b}{c} + \frac{c}{a} \overbrace{\geq}^{AM-GM} 3 \] \[ \sum_{\text{cyc}} a^3b^2c = a^3b^2c + b^3c^2a + c^3a^2b \overbrace{\geq}^{AM-GM} 3(abc)^2 \] \[ \sum_{\text{cyc}} \frac{c+ab+1}{1+a+a^2} = \frac{c+ab+1}{1+a+a^2}+\frac{a+bc+1}{1+b+b^2}+\frac{b+ca+1}{1+c+c^2} \ge 3 \]
In contrast, a symmetrical inequality is one that remains unchanged under any permutation of its variables. A function \(f(a,b,c)\) is said to be symmetric if it satisfies:
\[ \underbrace{f(a,b,c)=f(a,c,b)=f(b,a,c)=f(b,c,a)=f(c,a,b)=f(c,b,a)}_{3! \quad \text{permutations}} \]
In other words, any swap or rearrangement of \(a, b, c\) leaves the function invariant. This complete symmetry is denoted by the notation: \(\sum_{\text{sym}}\), which indicates summing over all distinct permutations of the variables.
Consider the following examples:
\[ \sum_{\text{sym}} a = a + a + b + b + c + c \overbrace{\geq}^{AM-GM} 6\cdot\sqrt[3]{abc} \] \[ \sum_{\text{sym}} a^2b = a^2b + a^2c + b^2c + b^2a + c^2a + c^2b \overbrace{\geq}^{AM-GM} 6 \cdot abc \]
To highlight the difference, compare the following two sums:
Another comparison:
These examples illustrate how the cyclic and symmetrical sum notations capture different patterns of symmetry within inequalities. While cyclic sums rotate the variables in a fixed order, symmetrical sums account for every possible permutation, reflecting complete invariance under any swap of the variables.
Grouping terms
Solving more complex inequality problems requires more than just applying the general formula. A common approach involves strategically grouping terms to our advantage, then applying the Arithmetic Mean-Geometric Mean (AM-GM) inequality—or another relevant inequality—to each group. Finally, we combine the resulting inequalities to form a larger, more powerful inequality.
With practice, this technique will become second nature. However, at first glance, it may seem unintuitive.
Can you solve the following problems without relying on any hints?
Let \( a,b,c \in \mathbb{R}_{+} \). Prove the inequality:
\[ (a^2+bc)(b^2+ca)(c^2+ab) \ge 8(abc)^2 \]
Hint 1
Apply the Arithmetic Mean-Geometric Mean (AM-GM) inequality to each pair of terms as follows:
\(a^2+bc\ge2\sqrt{a^2bc}\)
Solution
This is a classic problem where we group terms and apply the AM-GM inequality to each group individually. First, we apply the AM-GM inequality to each pair of terms:
\[ \begin{cases} a^2+bc\ge2\sqrt{a^2bc} = 2a\sqrt{bc} \\ b^2+ac\ge2\sqrt{b^2ac} = 2b\sqrt{ac} \\ c^2+ab\ge2\sqrt{c^2ab} = 2c\sqrt{ab} \end{cases} \]
Next, multiplying these inequalities together (since all terms are positive), we get:
\[ \underbrace{(a^2+bc)}_{\ge 2a\sqrt{bc}}\underbrace{(b^2+ac)}_{\ge 2b\sqrt{ac}}\underbrace{(c^2+ab)}_{\ge 2c\sqrt{ab}}\ge8abc\sqrt{a^2b^2c^2}=8(abc)^2 \]
Thus, the inequality is proven.
Equality holds when \(a=b=c=1\).
Let \(x,y,z\) positive real numbers, and \((1+x)(1+y)(1+z)=8\), prove that \(xyz \le 1\).
Hint 1
The terms in the product are already grouped for us.
Solution
We apply the Arithmetic Mean-Geometric Mean (AM-GM) inequality to each term in the product:
\[ (1+x) \ge 2\sqrt{x}, (1+y) \ge 2\sqrt{y} \text{ and } (1+z) \ge 2\sqrt{z} \]
Thus, we have:
\[ 8 = \underbrace{(1+x)}_{\ge 2\sqrt{x}}\underbrace{(1+y)}_{\ge 2\sqrt{y}}\underbrace{(1+z)}_{\ge2\sqrt{z}} \ge 8\sqrt{xyz} \]
Since we are given \((1+x)(1+y)(1+z)=8\), it follows that:
\[ 8 \ge 8 \sqrt{xyz} \Leftrightarrow 1 \ge xyz \]
Hence, the inequality is proven. Equality holds true when \(x=y=z=1\).
Let \(x_i \in \mathbb{R}_{+}\), where \(n\) is an even natural number and \(\prod_{i=1}^nx_i=1\). Prove that:
\((x_1^2+x_2^2)(x_3^2+x_4^2)\dots(x_{n-1}^2+x_{n}^2)\ge 2^{\frac{n}{2}}\)
Hint 1
The terms are already grouped for us. Consider applying the Arithmetic Mean-Geometric Mean (AM-GM) inequality to each group.
Solution
We apply the AM-GM inequality to each pair of terms:
\[ \begin{cases} x_1^2+x_2^2 \ge 2x_1x_2 \\ x_3^2+x_4^2 \ge 2x_3x_4 \\ \dots \\ x_{n-1}^2+x^{n} \ge 2x_{n-1}x_n \end{cases} \]
In total there are \(\frac{n}{2}\) groups. Thus, we have:
\[ (x_1^2+x_2^2)\dots(x_{n-1}^2+x_{n}^2)\ge(\underbrace{2*\dots*2}_{\frac{n}{2}})\sqrt{\prod_{i=1}^n x_i} \]
Since \(\prod_{i=1}^{n}x_i=1\), this simplifies to:
\[ (x_1^2+x_2^2)\dots(x_{n-1}^2+x_{n}^2)\ge 2^{\frac{n}{2}} \]
Equality holds when \(x_1=x_2=\dots=x_n=1\).
Let \(x,y,z\) positive real numbers such that \(xyz=6\). Prove the inequality:
\[ \frac{2x}{(2x^2+y^2)(x^2+2z^2)}+\frac{3y}{(3y^2+z^2)(y^2+3x^2)}+\frac{5z}{(5z^2+x^2)(z^2+5y^2)} \leq \frac{1}{8} \]
Hint 1
The denominators are grouped in a way that suggests applying the Arithmetic Mean-Geometric Mean (AM-GM) inequality directly.
Solution
We apply the AM-GM inequality to bound each factor in the denominators:
\[ \frac{2x}{(2x^2+y^2)(x^2+2z^2)} \leq \frac{2x}{2\sqrt{2}xy \cdot 2\sqrt{2}xz} = \frac{1}{4\cdot xyx} = \frac{1}{24} \] \[ \frac{3y}{(3y^2+z^2)(y^2+3x^2)} \leq \frac{3y}{2\sqrt{3}zy \cdot 2\sqrt{3}yx} = \frac{1}{4\cdot xyz} = \frac{1}{24} \] \[ \frac{5z}{(5z^2+x^2)(z^2+5y^2)} \leq \frac{5z}{2\sqrt{5}zx \cdot 2\sqrt{5}zy} = \frac{1}{4\cdot xyz} = \frac{1}{24} \]
Summing the three inequalities proves the original.
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Galati, 2018
Let \(n\) a natural number greater than \(0\), prove that:
\[ \sqrt{1\cdot2}+\sqrt{2\cdot3}+\dots+\sqrt{n(n+1)} < n(n+1) \]
Solution
We first apply the AM-GM inequality term by term:
\[ \underbrace{\sqrt{1\cdot2}}_{< \frac{1+2}{2}}+\underbrace{\sqrt{2\cdot3}}_{< \frac{2+3}{2}}+\dots+\underbrace{\sqrt{n(n+1)}}_{< \frac{n+n+1}{2}} < \] \[ < 1+2+\dots+n+\frac{n}{2} = \frac{n(n+2)}{2} \overbrace{<}^{?} n(n+1) \]
It remains to show \(\,\frac{n\,(n+2)}{2} < n(n+1)\). Multiply both sides by 2:
\[ n\,(n+2) \;<\; 2n\,(n+1). \]
Dividing by \(n\) (which is positive) simplifies to \(\,n+2 < 2(n+1)\), or \(\,n + 2 < 2n + 2\), which is true for all \(n>0\). Thus \(\,\frac{n\,(n+2)}{2} < n(n+1)\), completing the proof.
Source
Romanian Math Olympiad, Etapa Locala, 8th grade, Caras-Severin, 2013 (Laurentiu Panaitopol)
Let \(n \in \mathbb{N}^{*}\) such that \(n\gt1\), prove the inequality:
\[ n^3+n^2+2n \gt 4\sqrt{n}(1+\sqrt{2}+\dots+\sqrt{n}) \]
Solution
First, factor out terms to reveal a pattern:
\[ n^3+n^2+2n \gt 4\sqrt{n}(1+\sqrt{2}+\dots+\sqrt{n}) \Leftrightarrow \] \[ \Leftrightarrow n\cdot\frac{n(n+1)}{1}+2n \gt 4\left(\sqrt{n}+\sqrt{2n}+\dots+\sqrt{n^2}\right) \]
Dividing both sides by \(2\), the inequality becomes:
\[ n\cdot(1+\dots+n)+(\underbrace{1+\dots+1}_{=n}) \gt 2(\sqrt{n}+\sqrt{2n}+\dots+\sqrt{n\cdot n}) \] \[ (n + 1) + (2n + 1) + \dots + (n\cdot n + 1) \gt 2(\sqrt{n}+\sqrt{2n}+\dots+\sqrt{n\cdot n}) \]
We claim that each group \((k n + 1)\) is at least \(2\sqrt{k n}\) by the AM-GM inequality::
\[ \begin{cases} n+1 \overbrace{\geq}^{\text{AM-GM}} 2\sqrt{n} \\ 2n+1 \overbrace{\geq}^{\text{AM-GM}} 2\sqrt{2n} \\ \dots \\ n\cdot n + 1 \overbrace{\geq}^{\text{AM-GM}} 2\sqrt{n\cdot n} \end{cases} \]
Summing these inequalities for \(k\) from 1 to \(n\) yields exactly the required inequality. When summing the inequalities, the equality condition is lost due to the fact that there's no such \(n\) so that all weak inequalities hold (in the same time).
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Galati, 2005
The next problem is more difficult to solve but a previous exercise might help:
Let \(n \in \mathbb{N}\setminus\{0,1\}\). Prove the inequality:
\[ \frac{1}{5+2^4}+\frac{1}{5+3^4}+\frac{1}{5+4^4}+\dots+\frac{1}{5+n^4} \lt \frac{n-1}{4\cdot n} \]
Hint 1
In a previous exercise, we proved that: \(a^4+b^4+1 \geq 2b^2a\sqrt{2}\) by applying the AM-GM inequality twice:
\[ a^4+b^4+1 = (a^4+1) + b^4 \geq 2a^2+b^4 \geq 2\sqrt{2}b^2a \]
Hint 2
Observe that each term can be written in the form:
\[ \frac{1}{5+k^4} = \frac{1}{\left(\sqrt{4}\right)^4+k^4 + 1} \leq \text{?} \]
Hint 3
Approximate the resulting sum with a telescoping series.
Solution
From a previous result, we have: \(a^4+b^4+1 \geq 2b^2a\sqrt{2}\) by applying the AM-GM inequality twice:
\[ a^4+b^4+1 = (a^4+1) + b^4 \geq 2a^2+b^4 \geq 2\sqrt{2}b^2a \]
We can apply this giving:
\[ \frac{1}{5+2^4}+\frac{1}{5+3^4}+\frac{1}{5+4^4}+\dots+\frac{1}{5+n^4} = \] \[ = \frac{1}{\left(\sqrt{4}\right)^4+2^4+1}+\frac{1}{\left(\sqrt{4}\right)^4+3^4+1}+\dots+\frac{1}{\left(\sqrt{4}\right)^4+n^4+1} \leq \] \[ \leq \frac{1}{2\cdot\sqrt{2}\cdot 2^2 \cdot \sqrt{2}} + \leq \frac{1}{2\cdot\sqrt{2}\cdot 3^2 \cdot \sqrt{2}} + \dots + \frac{1}{2\cdot\sqrt{2}\cdot n^2 \cdot \sqrt{2}} \leq \] \[ \frac{1}{4}(\frac{1}{2^2}+\frac{1}{3^2}+\dots+\frac{1}{n^2}) \]
So, what we know so far is that:
\[ \begin{align} \sum_{i=2}^n \frac{1}{5+i^4} \leq \frac{1}{4}\left(\sum_{i=2}^n \frac{1}{i^4} \right) \end{align} \]
However, a cleaner bound can be obtained by noting: \( \frac{1}{i^2} < \frac{1}{(i-1)\cdot i}\). Using this in \((1)\) leads to:
\[ \begin{align} \sum_{i=2}^n \frac{1}{5+i^4} \leq \frac{1}{4}\left(\sum_{i=2}^n \frac{1}{i^4} \right) \lt \frac{1}{4} \left(\sum_{i=2}^n \frac{1}{(i-1)\cdot i}\right) \tag{2} \end{align} \]
We now evaluate the telescoping sum:
\[ \frac{1}{4} \left(\sum_{i=2}^n \frac{1}{(i-1)\cdot i}\right) = \frac{1}{4} \left(\frac{1}{1\cdot 2}+\frac{1}{2 \cdot 3} + \dots + \frac{1}{(n-1) \cdot n}\right) = \] \[ \begin{align} = \frac{1}{4}\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\dots+\frac{1}{n-1}-\frac{1}{n}\right) = \frac{1}{4}\left(1-\frac{1}{n}\right) = \frac{n-1}{4\cdot n} \tag{3} \end{align} \]
Therefore, introducing \((3)\) in \((2)\) proves our inequality:
\[ \sum_{i=2}^n \frac{1}{5+i^4} \leq \frac{1}{4}\left(\sum_{i=2}^n \frac{1}{i^4} \right) \lt \frac{1}{4} \left(\sum_{i=2}^n \frac{1}{(i-1)\cdot i}\right) = \frac{n-1}{4\cdot n} \]
Source
Romanian Math Olympiad, Etapa Locala, 8th grade, Galati, 2019
Remember, the key to solving the next problem is to leverage the additional condition to your advantage. While the terms may already be “grouped” for you, this alone won’t be sufficient.
Let \(a,b,c\) positive real numbers such that \(a+b+c=1\). Prove the inequality:
\[ \Bigl(\frac{1}{a}-1\Bigl)\Bigl(\frac{1}{b}-1\Bigl)\Bigl(\frac{1}{c}-1\Bigl) \ge 8 \]
Hint 1
Rewrite each term in the following form:
\[\frac{1}{a}-1=\frac{1-a}{a} \]
Hint 2
Using \(a+b+c=1\), we can express \(a = 1-b-c\), and consequently
\[ \frac{1}{a}-1=\frac{1-a}{a}=\frac{b+c}{a} \]
Solution
Taking the above hints into account, we proceed as follows:
\[ \Bigl(\frac{1}{a}-1\Bigl)\Bigl(\frac{1}{b}-1\Bigl)\Bigl(\frac{1}{c}-1\Bigl) = \frac{\overbrace{b+c}^{\ge2\sqrt{bc}}}{a} * \frac{\overbrace{a+c}^{\ge2\sqrt{ac}}}{b} * \frac{\overbrace{a+b}^{\ge2\sqrt{ab}}}{c} \]
By applying the AM-GM inequality to each term:
\[ b+c \ge 2\sqrt{bc} , a+c \ge 2\sqrt{ac} \text{ and } a+b \ge 2\sqrt{ab} \]
We obtain:
\[ \frac{\overbrace{b+c}^{\ge2\sqrt{bc}}}{a} * \frac{\overbrace{a+c}^{\ge2\sqrt{ac}}}{b} * \frac{\overbrace{a+b}^{\ge2\sqrt{ab}}}{c} \ge \frac{2\sqrt{bc}}{a} * \frac{2\sqrt{ac}}{b} * \frac{2\sqrt{ab}}{c} = \frac{8\sqrt{a^2b^2c^2}}{abc}=8 \]
Equality holds when \(a+b+c=1\) and \(a=b=c\). To satisfy both conditions \(a=b=c=\frac{1}{3}\).
The next problem, proposed by Dorin Marghidanu, is a generalisation of the previous one, but can you “spot” the similarity?
If \(0 \lt a_1, a_2, \dots, a_n \leq 1\), such that \(a_1+a_2+\dots+a_n=n-1\), then:
\[ (n-1)^n \cdot (1-a_1) \cdot (1-a_2) \cdot \dots \cdot (1-a_n) \leq a_1 a_2 \dots a_n \]
Hint 1
This substitution simplifies the inequality into a more recognizable form.
Try letting \(a_i = 1 - b_i\).
In this regard, why don't you write \(a_i=1-b_i\)?
Solution
We define \(a_i = 1 - b_i\). This is valid because \(a_i \in (0, 1]\) implies \(b_i \in [0, 1)\), and since \(a_i > 0\), we know \(b_i < 1\):
\[ n-1=\sum_{i=1}^n a_i = \sum_{i=1}^n \left(1-b_i\right) = n - \sum_{i=1}^n b_i \Rightarrow \] \[ \sum_{i=1}^n b_i = 1 \]
Substituting back into the inequality, the left-hand side becomes:
\[ \left(n-1\right)^n * \prod_{i=1}^n b_i \leq \prod_{i=1}^n \left(1-b_i\right) \Leftrightarrow \]
Now divide both sides by \(\prod b_i\) (which is positive), to get:
\[ \prod_{i=1}^n \left(\frac{1-b_i}{b_i}\right) \geq (n-1)^n \]
This is the key inequality. It can be proven using the AM-GM inequality. Here's the outline:
Each term \(\frac{1 - b_i}{b_i}\) can be written as \(\frac{\sum_{j \ne i} b_j}{b_i}\). Since \(\sum b_i = 1\), we know \(\sum_{j \ne i} b_j = 1 - b_i\):
Using AM-GM on each numerator:
\[ \frac{b_2+b_3+\dots+b_n}{b_1} + \frac{b_1+b_3+\dots+b_n}{b_2} + \dots + \frac{b_1+\dots+b_{n-1}}{b_n} \geq \] \[ \frac{(n-1)\sqrt[(n-1)]{b_2*\dots*b_n}}{b_1} + \dots + \frac{(n-1)\sqrt[(n-1)]{b_1*\dots*b_{n-1}}}{b_n} \]
Using the AM-GM inequality again:
\[ \frac{(n-1)\sqrt[n-1]{b_2*\dots*b_n}}{b_1} + \dots + \frac{(n-1)\sqrt[n]{b_1*\dots*b_{n-1}}}{b_n} \geq \] \[ \frac{(n-1)^n\sqrt[n-1]{\prod_{i=1}^n b_i}}{\prod_{i=1}^n b_i} = (n-1)^n \]
Thus, the inequality is proven.
Source
Dorin Marghidanu
The next problem is another generalisation of an exercise proposed to the Romanian (Olympiad) Team Selection Test from 2002:
Let \(k, x_1, x_2, \dots, x_n \in (0,1)\) such that \(k \gt \max\{x_1, x_2, \dots, x_n\}\). Prove the following inequality:
\[ \sqrt{\prod_{i=1}^n x_i} + \sqrt{\prod_{i=1}^n(k-x_i)} \lt k \]
Hint 1
If \(a\in (0,1)\) then \(\sqrt{a}\lt\sqrt[3]{a}\).
Solution
Since \(x_1, x_2, \dots, x_n \in (0,1)\) and \(k \in (0,1)\) then \(\prod x_i \in (0,1)\) and \(\prod (k-x_i) \in (0,1)\).
Taking this into consideration:
\[ \begin{align} \sqrt{\prod_{i=1}^n x_i} \leq \sqrt[n]{\prod_{i=1}^n x_i} \overbrace{\leq}^{AM-GM} \frac{1}{n} \cdot \sum_{i=1}^n x_i \tag{1} \end{align} \]
In the same time, by applying the AM-GM inequality:
\[ \begin{align} \sqrt{\prod_{i=1}^n(k-x_i)} \leq \sqrt[n]{\prod_{i=1}^n(k-x_i)} \overbrace{\leq}^{AM-GM} \frac{1}{n}\cdot \sum_{i=1}^n (k-x_i) \tag{2} \end{align} \]
After summing \((1)\) and \((2)\), our initial inequality is proven:
\[ \sqrt{\prod_{i=1}^n x_i} + \sqrt{\prod_{i=1}^n(k-x_i)} \leq \frac{1}{n}\cdot \sum_{i=1}^n x_i + \frac{1}{n}\cdot \sum_{i=1}^n (k-x_i) \Leftrightarrow \] \[ \sqrt{\prod_{i=1}^n x_i} + \sqrt{\prod_{i=1}^n(k-x_i)} \leq \frac{1}{n}\cdot \sum_{i=1}^n x_i + k - \frac{1}{n}\cdot \sum_{i=1}^n x_i = k \]
Source
Romanian Team Selection Test, 2002, generalisation
Let \(a,b,c\) be positive real numbers such that \(a^3+b^3+c^3=3\). Prove the inequality:
\[ \frac{a(1-a)}{(1+b)(1+c)} + \frac{b(1-b)}{(1+a)(1+c)} + \frac{c(1-c)}{(1+a)(1+b)} \le 0 \]
Hint 1
Consider rewriting the expression with a common denominator.
Solution
First, we combine the terms over a common denominator:
\[ \frac{a(1-a)}{(1+b)(1+c)} + \frac{b(1-b)}{(1+a)(1+c)} + \frac{c(1-c)}{(1+a)(1+b)} = \\ = \frac{(a+b+c)-(a^3+b^3+c^3)}{(1+a)(1+b)(1+c)} \le 0 \]
Since \((1+a)(1+b)(1+c)\gt 0\), it suffices to show that:
\[ a^3+b^3+c^3 \ge a + b + c \]
We apply the AM-GM inequality to each of the terms::
\[ \begin{cases} a^3 + 1 + 1 \ge 3a \\ b^3 + 1 + 1 \ge 3b \\ c^3 + 1 + 1 \ge 3c \end{cases} \]
Summing these inequalities gives:
\[ (a^3+b^3+c^3)+6 \ge 3(a+b+c) \]
Since \(a^3+b^3+c^3=3\), we have:
\[ 3 + 6 \ge 3 (a+b+c) \Leftrightarrow 3 \ge a+b+c \]
Thus, we conclude:
\[ a^3+b^3+c^3 \ge 3 \ge a+b+c \]
Equality holds when \(a=b=c=1\).
Source
Gheorghe Craciun - Facebook group "Comunitatea Profesorilor De Matematica"
We have already solved the following inequality using a different technique, but can you now prove it again by applying ‘grouping’ and the AM-GM inequality?
Let \(x,y,z\) positive real numbers. Prove that:
\[ x^2+y^2+z^2 \ge xy + yz + zx \]
Hint 1
Multiply both sides of the inequality by \(2\), then group the terms and apply the AM-GM inequality to each group.
Solution
By multiplying both sides of the inequality by \(2\), we obtain the equivalent inequality::
\( \underbrace{(x^2+y^2)}_{\ge 2xy}+\underbrace{(y^2+z^2)}_{\ge 2yz}+\underbrace{(z^2+x^2)}_{\ge 2zx} \ge 2(xy + yz + zx) \Leftrightarrow \\ x^2 + y^2 + z^2 \ge xy + yz + zx \)
Now, applying the AM-GM inequality to each pair of terms:
\[ \begin{cases} x^2 + y^2 \ge 2xy \\ y^2 + z^2 \ge 2yz \\ z^2 + x^2 \ge 2zx \end{cases} \]
Summing the results:
\[ 2(x^2 + y^2 + z^2) \ge 2(xy + yz+zx) \Leftrightarrow x^2 + y^2 + z^2 \ge xy + yz + zx \]
Equality holds when \(x=y=z\).
Let \(x,y,z\) positive real numbers. Prove that
\[ x^2+y^2+z^2 \ge x\sqrt{yz}+y\sqrt{zx}+z\sqrt{xy} \]
Hint 1
We have already proven that: \(x^2+y^2+z^2\ge xy+yz+zx\)
Hint 2
We can apply the AM-GM inequality to the following pairs of terms::
\[xy+yz \ge 2y\sqrt{xz}\]
Solution
First, we observe that we have already proven:
\[ x^2+y^2+z^2 \ge xy + yz + zx \]
Thus, it is sufficient to prove that:
\[ xy + yz + zx \ge x\sqrt{yz}+y\sqrt{zx}+z\sqrt{xy} \]
Applying the AM-GM inequality to the following pairs::
\[ \begin{cases} xy+yz \ge 2y\sqrt{xz} \\ yz+zx \ge 2z\sqrt{xy} \\ zx+xy \ge 2x\sqrt{zy} \end{cases} \]
Summing these inequalities:
\[ 2(xy+yz+zx) \ge 2(x\sqrt{yz}+y\sqrt{zx}+z\sqrt{xy}) \Leftrightarrow \\ xy+yz+zx \ge x\sqrt{yz}+y\sqrt{zx}+z\sqrt{xy} \]
Therefore::
\[ \boldsymbol{x^2+y^2+z^2} \ge xy + yz + zx \ge \boldsymbol{x\sqrt{yz}+y\sqrt{zx}+z\sqrt{xy}} \]
Equality holds for \(x=y=z=1\).
Let \(a,b,c\) positive real numbers, prove:
\[ a^3+b^3+c^3 + 3 \ge a+b+c+ab+bc+ca \]
Hint 1
Consider applying the AM-GM inequality to the following form:
\[x^3+y^3+1 \ge 3xy\]
Hint 2
Alternatively, apply the AM-GM inequality to this form:
\[x^3+1+1 \ge 3x\]
Solution
We begin by applying the AM-GM inequality to the following groups of terms:
\[ \begin{cases} a^3+b^3+1 \ge 3ab \\ b^3+c^3+1 \ge 3bc \\ c^3+a^3+1 \ge 3ca \\ \end{cases} \] and \[ \begin{cases} a^3+1+1 \ge 3a \\ b^3+1+1 \ge 3b \\ c^3+1+1 \ge 3c \end{cases} \]
Now, summing all the inequalities:
\[ 3(a^3+b^3+c^3+3) \ge 3(a+b+c+ab+bc+ca) \Rightarrow \\ \Rightarrow a^3+b^3+c^3 + 3 \ge a + b + c + ab + bc + ca \]
The equality holds if \(a=b=c=1\).
Source
Romanian Math Olympiad, Etapa Locala, 10th grade, Dolj, 2013
Can we make a short generalisation?
Let \(a,b,c,d\) positive real numbers and \(n \in \mathbb{N}^{*}\), prove that:
\[ \frac{a^n+b^n+c^n+d^n}{n} \geq a+b+c+d+2 - 2n \]
Hint 1
Use the AM-GM inequality in a creative way by adding several \(1\)s. For instance, to relate \(a^4\) back to \(a\), you can write:
\[ a^4+1+1+1 \overbrace{\geq}^{\text{AM-GM}} 4\cdot a \]
Generalize this idea to handle \(a^n\) by adding exactly \(\frac{n(n-1)}{2}\), so that the total number of terms matches n when applying AM-GM.
Solution
Apply the following "trick" to each of the variables \(a\), \(b\), \(c\), and \(d\):
\[ a^n + \overbrace{\underbrace{(1+\dots+1)}_{=\frac{(n-1)n}{2}}}^{(n-1)\quad \text{terms}} \overbrace{\geq}^{\text{AM-GM}} n \cdot a \]
Here, by design, you have \(1\) copy of \(a^n\) and \(\frac{n(n-1)}{2}\) copies of \(1\). You then group them in a way that AM–GM has n factors total, producing the factor \(n\,a\) on the right.
Summing these inequalities for \(a, b, c,\) and \(d\) gives:
\[ a^n + b^n + c^n + d^2 + 4 * \frac{(n-1) \cdot n}{2} \geq n \cdot (a+b+c+d) \]
Divide both sides by \(n\):
\[ \frac{\sum_{\text{cyc}} a^n}{n} + 2n-2 \geq \sum_{\text{cyc}} a \Leftrightarrow \] \[ \frac{\sum_{\text{cyc}} a^n}{n} \geq \sum_{\text{cyc}}a + 2-2n \]
This is exactly the desired inequality.
By AM-GM, equality holds only if all the terms we used are equal. In the step \[ a^n + 1 + 1 + \dots + 1 = n\,a, \] it forces \(a^n = 1\) and also each “1” must match \(a^n\). Consequently, \(a = 1\). The same argument applies to \(b, c,\) and \(d\), so all must be 1. Thus the inequality is sharp exactly when \(a=b=c=d=1\).
In a somewhat similar fashion:
Let \(a,b,c \in (0,1]\), and n natural number \(\geq 2\) prove that:
\[ \frac{c}{a^n + b^n + 3n-2} + \frac{a}{b^n+c^n+3n-2} + \frac{b}{c^n+a^n+3n-2} \leq \frac{1}{n} \]
Hint 1
We observe that:
\[ a^n + \underbrace{1+1+\dots+1}_{n-1 \quad \text{terms}} \overbrace{\geq}^{\text{AM-GM}} n \cdot a \]
Solution
For each term:
\[ \frac{c}{a^n + b^n + 3n-2} = \frac{c}{a^n+\underbrace{(1+\dots+1)}_{n-1}+b^n+\underbrace{(1+\dots+1)}_{n-1}+n} \leq \] \[ \frac{c}{an+bn+n} \tag{1} \]
Since \(c \in (0,1)\) then \(n \geq n \cdot c\). Introducing this in \((1)\):
\[ \frac{c}{a^n + b^n + 3n-2} \leq \frac{c}{an+bn+n} \leq \frac{c}{na + nb + nc} = \frac{c}{n(a+b+c)} \]
With this in mind, we can write the inequality as:
\[ \frac{c}{a^n + b^n + 3n-2} + \frac{a}{b^n+c^n+3n-2} + \frac{b}{c^n+a^n+3n-2} \leq \] \[ \frac{c}{n(a+b+c)}+\frac{b}{n(a+b+c)}+\frac{a}{n(a+b+c)} \leq \frac{a+b+c}{n(a+b+c)} = \frac{1}{n} \]
Source
Andrei N. Ciobanu
Let \(a,b,c \in \mathbb{R}_{+}\). Prove that:
\[ a^3+b^3+c^3 \ge \frac{3}{2}(ab+bc+cd-1) \]
Hint 1
Consider applying the AM-GM inequality to the following groups \(\{a^3, b^3, \text{?}\}\), \(\{?, b^3, c^3\}\) and \(\{a^3, ?, c^3\}\)
Solution
We apply the AM-GM inequality to the following terms:
\[ \begin{cases} a^3+b^3+1 \ge 3\sqrt[3]{a^3b^3} = 3ab \\ b^3+c^3+1 \ge 3\sqrt[3]{b^3c^3} = 3bc \\ c^3+a^3+1 \ge 3\sqrt[3]{c^3a^3} = 3ca \end{cases} \]
Next, we sum the inequalities::
\[ 2(a^3+b^3+c^3) + 6 \ge 3(ab+bc+ca) \Leftrightarrow \\ a^3+b^3+c^3 \ge \frac{3}{2}(ab+bc+ca-1) \]
The equality holds if \(a=b=c=1\).
Source
Concursul Gazeta Matematica, 9th grade, 12th edition, Romania
Let \(a,b,c \in \mathbb{R}_+\), prove:
\[ a^3+b^3+c^3 \ge \frac{1}{3} (a+b+c)(ab+bc+ca) \]
Hint 1
Recall that we have already proven the following:
\[a^3+b^3 \ge ab(a+b)\]
Hint 2
By applying the AM-GM inequality, we can also conclude:
\[a^3+b^3+c^3\ge 3abc\]
Solution
We start by applying the inequalities derived earlier:
\[ \begin{cases} a^3 + b^3 \ge ab(a+b) \\ b^3 + c^3 \ge bc(b+c) \\ c^3 + a^3 \ge ca(c+a) \\ \end{cases} \]
Additionally, we have the inequality:
\[ a^3+b^3+c^3 \ge 3abc \]
Next, we sum all of these inequalities:
\[ 3(a^3+b^3+c^3) \ge ab(a+b) + abc + bc(b+c) + abc + ca(c+a) + abc \\ a^3+b^3+c^3 \ge \frac{1}{3}(a+b+c)(ab+bc+ca) \]
Equality holds when \(a=b=c=1\).
The next two problems can be easily solved using an inequality that we will discuss shortly. However, let’s first attempt to solve them using the AM-GM inequality, employing a strategy similar to the one we used earlier:
Let \(x,y,z \in (0, \infty)\). Prove:
\[ \frac{x^3}{y}+\frac{y^3}{z}+\frac{z^3}{x} \ge x^2 + y^2 + z^2 \]
Hint 1
By applying the AM-GM inequality, we know::
\[ \frac{x^3}{y}+xy \ge 2x^2 \]
Solution
We start by applying the AM-GM inequality to each pair of terms:
\[ \begin{cases} \frac{x^3}{y}+xy \ge 2x^2 \\ \frac{y^3}{z}+yz \ge 2y^2 \\ \frac{z^3}{x}+zx \ge 2z^2 \end{cases} \]
Next, summing the inequalities:
\[ \frac{x^3}{y}+\frac{y^3}{z}+\frac{z^3}{x} + (xy+yz+zx) \ge (x^2+y^2+z^2) + (x^2+y^2+z^2) \]
Since \(x^2 + y^2 + z^2 \ge xy + yz + zx\), we obtain:
\[ \frac{x^3}{y}+\frac{y^3}{z}+\frac{z^3}{x} + (xy+yz+zx) \ge (x^2+y^2+z^2) + (x^2+y^2+z^2) \ge \\ \ge (x^2+y^2+z^2) + (xy + yz + zx) \Rightarrow \\ \Rightarrow \frac{x^3}{y}+\frac{y^3}{z}+\frac{z^3}{x} \ge x^2+y^2+z^2 \]
The equality holds if \(x=y=z\).
Source
Concursul Gazeta Matematica si Viitori Olimpici, 9th grade, Edition X, Romania
Let \(x,y,z\) positive real numbers, prove:
\[ \frac{x^2+\sqrt{yz}}{2\sqrt{yz}}+\frac{y^2+\sqrt{zx}}{2\sqrt{zx}}+\frac{z^2+\sqrt{xy}}{2\sqrt{xy}} \ge \sqrt{x}+\sqrt{y}+\sqrt{z} \]
Hint 1
An equivalent way to write the inequality is:
\[ \frac{x^2}{\sqrt{yz}}+\frac{y^2}{\sqrt{zx}}+\frac{z^2}{\sqrt{xy}}+3 \ge 2(\sqrt{x}+\sqrt{y}+\sqrt{z}) \]
Solution
We begin by rewriting the inequality as:
\[ \frac{x^2}{\sqrt{yz}}+\frac{y^2}{\sqrt{zx}}+\frac{z^2}{\sqrt{xy}}+3 \ge 2(\sqrt{x}+\sqrt{y}+\sqrt{z}) \]
Next, we apply the AM-GM inequality to the following terms:
\[ \begin{cases} \frac{x^2}{\sqrt{yz}}+\sqrt{y}+\sqrt{z}+1 \ge 4\sqrt{x} \\ \frac{y^2}{\sqrt{zx}}+\sqrt{z}+\sqrt{x}+1 \ge 4\sqrt{y} \\ \frac{z^2}{\sqrt{xy}}+\sqrt{x}+\sqrt{y}+1 \ge 4\sqrt{z} \end{cases} \]
Summing all the inequalities leads to the desired result.
The equality holds when \(x=y=z=1\).
An important thing to take in consideration is that when we sum/multiply weak inequalities involving interdependent terms, we need to verify conditions across the inequalities to check if they remain consistent:
Let \( a,b,c \in> \mathbb{R}_{+} \) such that \(ab+bc+ca=1\). Prove that:
\[ a+b+c\gt\frac{2}{3}(\sqrt{1-ab}+\sqrt{1-bc}+\sqrt{1-ac}) \]
Hint 1
Apply the Arithmetic Mean-Geometric Mean (AM-GM) inequality in the following manner (for all terms):
\(\frac{a+(b+c)}{2}\ge\sqrt{a(b+c)}\)
Hint 2
Consider the fact that \(ab+bc+ca=1\). How might this help us?
Solution
We begin by grouping the terms and applying the AM-GM inequality three times:
\[ \begin{cases} \frac{a+(b+c)}{2} \ge \sqrt{a(b+c)} = \sqrt{ab+ac} \\ \frac{b+(a+c)}{2} \ge \sqrt{b(a+c)} = \sqrt{ba+bc} \\ \frac{c+(a+b)}{2} \ge \sqrt{c(a+b)} = \sqrt{ca+cb} \end{cases} \]
Next, we sum all the inequalities:
\[ \frac{3(a+b+c)}{2}\gt\sqrt{ab+bc}+\sqrt{ba+bc}+\sqrt{ca+bc} \]
Using the condition \(ab+bc+ca=1\), we can substitute the terms:
\[ \frac{3(a+b+c)}{2}\gt\sqrt{1-bc}+\sqrt{1-ac}+\sqrt{1-ab} \Leftrightarrow \\ a+b+c\gt\frac{2}{3}(\sqrt{1-bc}+\sqrt{1-ac}+\sqrt{1-ab}) \]
Furthermore, since \(a,b,c\) are positive real numbers, equality cannot hold.
Source
Andrei N. Ciobanu
Sometimes, we need to find creative ways to group terms. If you’re unable to find the solution right away, don’t worry—this inequality is quite challenging to solve using only the AM-GM inequality.
Let \(a,b,c \in (0,\infty)\) such that \(bc+ac+ca=abc\). Prove that:
\[ 3\sqrt{abc} \gt 2\sqrt{2}(\sqrt{a}+\sqrt{b}+\sqrt{c}) \]
Hint 1
Can you show that::
\[ \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1 \]
Hint 2
Consider applying the AM-GM inequality to the following groupings:
\[ \begin{cases} \frac{1}{a}+\frac{1}{a}+\frac{1}{b} = \frac{2}{a}+\frac{1}{b} \ge 2\sqrt{\frac{2}{ab}} \\ \frac{1}{b}+\frac{1}{b}+\frac{1}{c} = \frac{2}{b}+\frac{1}{c} \ge 2\sqrt{\frac{2}{bc}} \\ \frac{1}{c}+\frac{1}{c}+\frac{1}{a} = \frac{2}{c}+\frac{1}{a} \ge 2\sqrt{\frac{2}{ca}} \end{cases} \]
Solution
Start by dividing both sides of the equation \(abc=bc+ac+ab\) by \(abc\), which yields:
\[ \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1 \]
Next, apply the AM-GM inequality to the following groupings of terms::
\[ \frac{1}{a}+\frac{1}{a}+\frac{1}{b} = \frac{2}{a}+\frac{1}{b} \ge 2\sqrt{\frac{2}{ab}} \\ \frac{1}{b}+\frac{1}{b}+\frac{1}{c} = \frac{2}{b}+\frac{1}{c} \ge 2\sqrt{\frac{2}{bc}} \\ \frac{1}{c}+\frac{1}{c}+\frac{1}{a} = \frac{2}{c}+\frac{1}{a} \ge 2\sqrt{\frac{2}{ca}} \]
Summing these inequalities results in:
\[ 3(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}) \gt 2\sqrt{2}(\frac{1}{\sqrt{ab}} + \frac{1}{\sqrt{bc}}+\frac{1}{\sqrt{ca}}) \Leftrightarrow \\ 3 \gt 2\sqrt{2}(\frac{1}{\sqrt{ab}} + \frac{1}{\sqrt{bc}}+\frac{1}{\sqrt{ca}}) \Leftrightarrow \\ 3\sqrt{abc} \gt 2\sqrt{2}(\sqrt{c}+\sqrt{a}+\sqrt{b}) \]
Thus, the inequality holds.
Source
Andrei N. Ciobanu
Problems can become even more elegant when we apply strategic grouping to well-known identities. In this context, try solving the following exercise without relying on any hints:
Let \(a,b\in(0,\infty)\) and \(a-b\gt0\). Prove that:
\[a^3+b^3\gt 4ab\sqrt{b(a-b)}\]
Hint 1
Find an identity involving \(a^3+b^3\) and apply the AM-GM inequality.
Solution
We begin with the identity for the sum of cubes:
\[ a^3+b^3=(a+b)(a^2-ab+b^2) \]
Now, apply the AM-GM inequality to each factor:
\[ a^3+b^3=(\underbrace{a+b}_{\gt 2\sqrt{ab}})[\underbrace{(a^2-ab)+b^2}_{\gt 2b\sqrt{a(a-b)}}] \]
Since equality holds in AM-GM only if \(a=b\), and we know \(a-b\gt0\) the equality condition cannot be satisfied.
Multiplying the inequalities:
\[ a^3+b^3=(a+b)(a^2-ab+b^2) \gt 2\sqrt{ab} 2b \sqrt{a(a-b)} \Leftrightarrow \\ a^3+b^3 \gt 4ab\sqrt{b(a-b)} \]
Source
Andrei N. Ciobanu
At the end of this section, let’s refocus on some elegant weak inequalities:
Let \(x_1, x_2, \dots, x_n\) be positive real numbers. Prove that:
\[ 1+\sum_{j=2}^n[(\sum_{i=1}^j x_i) * (\sum_{i=1}^j \frac{1}{x_i})] \ge \frac{n(n+1)(2n+1)}{6} \]
Hint 1
Recall the formula for the sum of squares of the first \(n\) positive integers:
\[ 1^2+2^2+\dots+n^2 = \frac{n(n+1)(2n+1)}{6} \]
Hint 2
Expand the given expression as follows:
\[ 1+(x_1+x_2)(\frac{1}{x_1}+\frac{1}{x_2})+\dots+(x_1+\dots+x_n)(\frac{1}{x_1}+\dots+\frac{1}{x_n}) \ge \\ \ge \frac{n(n+1)(2n+1)}{6} \]
Solution
We begin by applying the Arithmetic Mean-Geometric Mean (AM-GM) inequality to the following expressions:
\[ \begin{cases} x_1+x_2+\dots+x_n \ge n\sqrt[n]{x_1 * x_2 * \dots * x_n} \\ \frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_n} \ge n\sqrt[n]{\frac{1}{x_1 * x_2 * \dots * x_n}} \end{cases} \]
Equality holds in both cases when \(x_1=x_2=\dots=x_n\). Thus, multiplying the two inequalities gives:
\[ (x_1+x_2+\dots+x_n)(\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_n}) \ge n^2 \sqrt[n]{\frac{x_1*x_2*\dots*x_n}{x_1*x^2*\dots*x_n}} = n^2 \]
Now, consider the terms in the original sum:
\[ 1+\underbrace{(x_1+x_2)(\frac{1}{x_1}+\frac{1}{x_2})}_{\ge 2^2}+\dots+\underbrace{(x_1+\dots+x_n)(\frac{1}{x_1}+\dots+\frac{1}{x_n})}_{\ge n^2} \ge \\ \ge 1 + \sum_{i=2}^n i^2 \ge \frac{n(n+1)(2n+1)}{6} \]
Therefore, the inequality is proven, and equality holds when \(x_1=x_2=\dots=x_n\).
Source
Andrei N. Ciobanu
Let \(n\in\mathbb{N}^{*}\) and \(x_1,\dots,x_n \in (0, \infty)\), satisfying the conditions:
\(S_1=\sum_{i=1}^n x_i = 9\) and \(S_2=\sum_{i=1}^n\frac{1}{x_i}=1\)
Find \(x_1,\dots,x_n\).
Hint 1
Can you use some techniques from the previous problem?
Solution
We apply the Arithmetic Mean-Geometric Mean (AM-GM) inequality to \(S_1\) and \(S_2\) and then multiply the two inequalities:
\[ S_1 * S_2 \ge n\sqrt[n]{x_1*\dots*x_n}*n\sqrt[n]{\frac{1}{x_1}*\dots*\frac{1}{x_n}} = n^2 \]
Thus we have:
\[ 9 \ge n^2 \Rightarrow n\in\{1,2,3\} \]
For \(n=1\) it is impossible because there is no \(x_1\) such that \(x_1=9\) and \(\frac{1}{x_1}=1\).
For \(n=2\) we need to solve the following system of equations:
\[ \begin{cases} x_1+x_2=9 \\ \frac{1}{x_1}+\frac{1}{x_2}=1 \end{cases} \]
Solving this system, we find two solutions:
\[ (x_1, x_2)\in\{(\frac{9+3\sqrt{5}}{2}, \frac{9-\sqrt{3}}{5}),(\frac{9-3\sqrt{5}}{2}, \frac{9+\sqrt{3}}{5})\} \]
For \(n=3\) the inequality becomes an equality, so \(x_1=x_2=x_3=3\).
Source
Concursul Gazeta Matematica, 6th Edition, 9th grade, Romania
The following problems are not primarily about grouping terms but rather about identifying “structures” where the AM-GM inequality can be applied to help move toward the solution:
Let \(a,b,c,d \in \mathbb{R}_{+}\) with \(a+b+c+d=k\), prove that:
\[ \frac{ab}{c+d+1}+\frac{bc}{a+d+1}+\frac{cd}{a+b+1}+\frac{da}{b+c+1} \lt k^2 \]
Hint 1
Recall the AM-GM inequality, which states:
\[ \sqrt{ab} \le \frac{a+b}{2} \Rightarrow ab \le \Bigl(\frac{a+b}{2}\Bigl)^2 \]
Hint 2
Using the AM-GM inequality, we can deduce that:
\[ ab \le \Bigl(\frac{a+b}{2}\Bigl)^2 \Leftrightarrow \frac{ab}{c+d+1} \le \Bigl(\frac{a+b}{2}\Bigl)^2 * \frac{1}{c+d+1} \]
Hint 3
Consider how the strict inequality may help in this case?
Solution
By applying the hints:
\[ \sum_{\text{cyc}} \frac{ab}{c+d+1} \le \sum_{\text{cyc}} \frac{(a+b)^2}{4*(c+d+1)} \lt \] \[ \lt \sum_{\text{cyc}} \frac{(a+b+c+d)^2}{4(c+d+1)} = \sum_{\text{cyc}} \frac{k^2}{4(c+d+1)} \lt \sum_{\text{cyc}} \frac{k^2}{4} = k^2 \]
Thus, the strict inequality is proven.
Let \(x,y,z\) be positive real numbers, prove that:
\[ \frac{x}{x+\sqrt{(x+y)(x+z)}}+\frac{y}{y+\sqrt{(y+z)(y+x)}}+\frac{z}{z+\sqrt{(z+x)(z+y)}} \le 1 \]
Hint 1
Can you prove the following inequality?
\[ \sqrt{(x+y)(x+z)}\ge\sqrt{xy}+\sqrt{xz} \]
Solution
To begin, we prove the inequality from Hint 1:
\[ \sqrt{(x+y)(x+z)}\ge\sqrt{xy}+\sqrt{xz} \]
Squaring both sides and applying the AM-GM inequality, we obtain:
\[ \sqrt{(x+y)(x+z)}\ge\sqrt{xy}+\sqrt{xz} \Leftrightarrow \\ (x+y)(x+z) \ge xy + zx + 2x\sqrt{yz} \Leftrightarrow \\ x^2 + xz+yx+yz \ge xy + zx + 2x\sqrt{yx} \Leftrightarrow \\ \frac{x^2+yz}{2} \ge x\sqrt{yz} \]
Next, applying this inequality to each term:
\[ \begin{cases} \frac{x}{x+\sqrt{(x+y)(x+z)}} \le \frac{x}{x+\sqrt{xy}+\sqrt{xz}} = \frac{\sqrt{x}}{\sqrt{x}+\sqrt{y}+\sqrt{z}} \\ \frac{y}{y+\sqrt{(y+z)(y+x)}} \le \frac{y}{y+\sqrt{yx}+\sqrt{yz}} = \frac{\sqrt{y}}{\sqrt{x}+\sqrt{y}+\sqrt{z}} \\ \frac{z}{z+\sqrt{(z+x)(z+y)}} \le \frac{z}{z+\sqrt{zx}+\sqrt{zy}} = \frac{\sqrt{z}}{\sqrt{x}+\sqrt{y}+\sqrt{z}} \end{cases} \]
Summing the three inequalities, we obtain:
\[ \frac{x}{x+\sqrt{(x+y)(x+z)}}+\frac{y}{y+\sqrt{(y+z)(y+x)}}+\frac{z}{z+\sqrt{(z+x)(z+y)}} \le \\ \le \frac{\sqrt{x}}{\sqrt{x}+\sqrt{y}+\sqrt{z}} + \frac{\sqrt{y}}{\sqrt{x}+\sqrt{y}+\sqrt{z}} + \frac{\sqrt{z}}{\sqrt{x}+\sqrt{y}+\sqrt{z}} = 1 \]
Thus, the inequality is proven. Equality holds if \(x=y=z=1\).
Source
This problem was sourced and adapted from the book: T. Andreescu, Z. Feng - 101 Problems in Algebra.
If \(a, b, c\) are real numbers greater than 1. Prove for any exponent \(r\gt0\), the sum:
\[ S = (\log_{a}bc)^r + (\log_{b}ca)^r + (\log_{c}ab)^r \ge 3*2^r \]
Hint 1
t is always useful to change to a common logarithm base:
\[\log_{a}bc=\frac{\ln bc}{\ln a}=\frac{\ln b}{\ln a}+\frac{\ln c}{\ln a}\]
Solution
First, express each logarithmic term in a common base using the natural logarithm:
\[ \begin{cases} \log_{a}bc=\frac{\ln b}{\ln a}+\frac{\ln c}{\ln a} \\ \log_{b}ca=\frac{\ln c}{\ln b}+\frac{\ln a}{\ln b} \\ \log_{c}ab=\frac{\ln a}{\ln c}+\frac{\ln b}{\ln c} \end{cases} \]
Next, apply the Arithmetic Mean-Geometric Mean (AM-GM) inequality:
\[ \begin{cases} \log_{a}bc=\frac{\ln b}{\ln a}+\frac{\ln c}{\ln a} \ge 2[\frac{\ln b \ln a}{(\ln a)^2}]^{\frac{1}{2}}\\ \log_{b}ca=\frac{\ln c}{\ln b}+\frac{\ln a}{\ln b} \ge 2[\frac{\ln c \ln a}{(\ln b)^2}]^{\frac{1}{2}}\\ \log_{c}ab=\frac{\ln a}{\ln c}+\frac{\ln b}{\ln c} \ge 2[\frac{\ln a \ln b}{(\ln c)^2}]^{\frac{1}{2}} \end{cases} \]
After raising each side to the power \(r\), we obtain:
\( \begin{cases} (\log_{a}bc)^r \ge 2^r[\frac{\ln b \ln a}{(\ln c)^2}]^{\frac{r}{2}}\\ (\log_{b}ca)^r \ge 2^r[\frac{\ln c \ln a}{(\ln b)^2}]^{\frac{r}{2}}\\ (\log_{c}ab)^r \ge 2^r[\frac{\ln a \ln b}{(\ln c)^2}]^{\frac{r}{2}} \end{cases} \)
Summing these inequalities:
\[ S \ge \frac{2^r(\ln b \ln a)^{\frac{r}{2}}}{(\ln a)^r}+\frac{2^r(\ln c \ln a)^{\frac{r}{2}}}{(\ln b)^r}+\frac{2^r(\ln a \ln b)^{\frac{r}{2}}}{(\ln c)^r} \]
Now, apply the AM-GM inequality again on the right-hand side:
\[ S \ge 3*[\frac{2^{3r}(\ln a \ln b \ln c)^r}{(\ln a \ln b \ln c)^r}]^{\frac{1}{3}}=3*2^r \]
Thus, we have shown that: \(S\ge3*2^r\).
When does the equality holds?
Source
Crux Mathematicorum, 1987, 202 (Proposed by D.S. Mitrinovic, solved by Murray Klamkin)
Let \(a,b,c\) positive real numbers such that \(abc=1\). Prove that:
\[ \left(a-1+\frac{1}{b}\right)\left(b-1+\frac{1}{c}\right)\left(c-1+\frac{1}{a}\right) \leq 1 \]
Hint 1
If \(abc=1\) it's always a good idea to perform the following substition (homogenisation):
\[ a=\frac{x}{y}, \quad b=\frac{y}{z}, \quad c=\frac{z}{x} \]
Solution
Since \(abc=1\) we can perform the following substition:
\[ a=\frac{x}{y}, \quad b=\frac{y}{z}, \quad c=\frac{z}{x} \]
The given inequality transforms and simplifies into/to:
\[ \left(\frac{x}{y}-1+\frac{z}{y}\right)\left(\frac{y}{z}-1+\frac{x}{z}\right)\left(\frac{z}{x}-1+\frac{y}{x}\right) \leq 1 \Leftrightarrow \\ (x-y+z)(y-z+x)(z-x+y) \leq xyz \]
Using the AM-GM inequality:
\[ (x-y+z)+(y-z+x) = 2x \geq 2\sqrt{(x-y+z)(y-z+x)} \\ (y-z+x)+(z-x+y) = 2y \geq 2\sqrt{(y-z+x)(z-x+y)} \\ (z-x+y)+(x-y+z) = 2z \geq 2\sqrt{(z-x+y)(x-y+z)} \\ \]
Multiplying all three inequalities:
\[ 8xyz \geq 8\sqrt{(x-y+z)^2(y-z+x)^2(z-x+y)^2} \Leftrightarrow \\ xyz \geq (x-y+z)(y-z+x)(z-x+y) \]
Thus, the inequality is proven.
Source
IMO 2000
Muirhead’s Theorem
Now that we’ve learned how to group and pair terms to our advantage, it’s time to introduce a powerful theorem used for symmetric inequalities, Muirhead’s theorem (named after Robert Muirhead).
Before delving into Muirhead’s theorem, we first need to understand the concept of majorisation.
Consider two sequences of numbers \(p=(p_1, p_2, \dots, p_n)\) and \(q=(q_1, q_2, \dots, q_n)\) aranged in decreasing order.
We say \(p\) majorises \(q\) (written as \(p \succ q\)), if the following two conditions hold:
- For each \(k\) from \(1\) to \(n-1\), the sum of the first \(k\) elements components of \(p\) is at least as large as that of \(q\): \[\sum_{i=1}^k p_i \geq \sum_{i=1}^k q_i\]
- The total of the sequences are equal:\[\sum_{i=1}^n p_i = \sum_{i=1}^n q_i\]
An example:
Consider the sequences:
\[p=(3,2,1), \quad q=(2,2,2)\]
We wish to determine if \(p \succ q\).
Solution
We check the partial sums:
\[ k = 1 \Rightarrow p_1 \geq q_1 \Leftrightarrow 3 \geq 2 \quad \textbf{\text{True}} \] \[ k = 2 \Rightarrow p_1 + p_2 \geq q_1 + q_2 \Leftrightarrow 5 \geq 4 \quad \textbf{\text{True}} \]
Since the partial sum conditions test holds, we test if the total sums are equal:
\[ p_1 + p_2 + p_3 \overbrace{=}^{?} q_1 + q_2 + q_3 \Leftrightarrow 6 = 6 \quad \textbf{\text{True}} \]
So yes, \(p \succ q\).
Now that we understand what majorisation is, let’s discuss Muirhead’s theorem:
If \(a_1, a_2, \dots, a_n\) are positive reals, and \(x_n\) majorises \(y_n\) then the following inequality is true:
\[ \sum_{\text{sym}} a_1^{x_1} * a_2^{x_2} * \dots *a_n^{x_n} \geq \sum_{\text{sym}}a_1^{y_1}*a_2^{y_2}*\dots*a_n^{y_n} \]
Note that Muirhead’s Inequality is “symmetrical” in nature, so it doesn’t work for “cyclic” inequalities.
For example let’s take the coefficients \((4,2,0)\) and \((3,2,1)\). We observe that the first sequences majorises the second, \((4,2,0) \succ (3,2,1)\).
In this regard, the following is true:
\[ \sum_{\text{sym}}a^4b^2 \geq \sum_{\text{sym}} a^3b^2c \Leftrightarrow \] \[ a^4b^2 + a^4c^2 + b^4a^2 + b^4c^2 + c^4a^2 + c^4b^2 \overbrace{\geq}^{Muir.} \] \[ \geq a^3b^2c + a^3c^2b + b^3a^2c + b^3c^2a + c^3b^2a + c^3a^2b \]
But the following is not true (by Muirhead’s inequality):
\[ \sum_{\text{cyc}}a^4b^2 \not\geq \sum_{\text{cyc}} a^3b^2c \Leftrightarrow \] \[ a^4b^2 + b^4c^2 + c^4a^2 \not\geq a^3b^2c + b^3c^2a + c^3a^2b \]
Now let’s solve two elementary inequalities, but this time without using “elementary” techniques or the AM-GM inequality. Use Muirhead’s Theorem instead:
Let \(a,b,c\) be positive real numbers. Prove that:
\[ a^2+b^2+c^2 \geq ab + bc + ca \]
Hint 1
Note that \(a^2\) can be written as \(a^2b^0c^0\).
Hint 2
Similarly, \(ab\) can be represented as \(a^1b^1c^0\).
Solution
We rewrite the inequality using exponent notation:
\[ a^2b^0c^0 + b^2a^0c^0+c^2b^0a^0 \geq a^1b^1c^0 + b^1a^1c^0 + c^1a^1b^0 \]
Observe that the exponent vector \((2,0,0) \succ (1,1,0)\), Thus, by applying Muirhead's theorem, we conclude that:
\[ \sum_{\text{sym}}a^2b^0c^0 \geq \sum_{\text{sym}} a^1b^1c^0 \Leftrightarrow \] \[ a^2 + a^2 + b^2 + c^2 + b^2 + c^2 \geq ab+ac+bc+ba+ca+cb \Leftrightarrow \] \[ 2(a^2+b^2+c^2) \geq 2(ab+bc+ca) \Leftrightarrow a^2+b^2+c^2 \geq ab + bc + ca \]
This completes the proof.
Let \(a,b,c\) positive real numbers. Prove the inequality:
\[ \frac{(a+b)(b+c)(c+a)}{abc} \geq 8 \]
Solution
We begin by expanding the numerator:
\[ (a+b)(b+c)(c+a) = a^2b + a^2c + b^2c+b^2a + c^2a + c^2b + abc + abc = \] \[ \begin{align} \sum_{\text{sym}} a^2b + 2abc \tag{1} \end{align} \]
We also note that:
\[ \begin{align} \sum_{\text{sym}} a^1 b^1 c^1 = 6 \cdot abc \Rightarrow abc = \frac{\sum_{\text{sym}} a^1b^1c^1}{6} \tag{2} \end{align} \]
Substituting expressions \((1)\) and \((2)\) into the original inequality gives:
\[ \frac{\sum_{\text{sym}} a^2b}{\frac{\sum_{\text{sym}} a^1b^1c^1}{6}} + 2 \geq 8 \Leftrightarrow \sum_{\text{sym}} a^2b^1c^0 \overbrace{\geq}^{?} \sum_{\text{sym}} a^1b^1c^1 \]
This is true because \( (2,1,0) \succ (1,1,1) \), and by Muirhead’s inequality, the symmetric sum on the left is greater than or equal to the one on the right.
Equality holds when \( a = b = c \).
Note: A more concise solution can be obtained using the AM-GM inequality.
\[ \frac{\prod_{\text{cyc}}(\overbrace{a+b}^{\geq 2\sqrt{ab}})}{abc} \overbrace{\geq}^{AM-GM} \frac{\prod_{\text{cyc}}(2\sqrt{ab})}{abc} \geq \frac{8\cdot abc}{abc} = 8 \]
I don’t want to overemphasize Muirhead’s Inequality because, although it’s a recognized theorem, its use is generally discouraged in math competitions. Moreover, any result you might prove using Muirhead can also be demonstrated with the more established AM-GM inequality. Think of Muirhead’s Inequality as a powerful, albeit somewhat brute-force, method to be used when other approaches fail… and only then.
The mean inequality chain
Also known as the QM-AM-GM-HM Inequalities, or how things are getting more serious.
Before presenting the actual inequality, let us first define two new types of means: the harmonic mean and the quadratic mean.
Let \(x_{i=1\dots n} \in \mathbb{R}_{+}\). Then, the following definitions hold::
\[ \text{Harmonic Mean}=\frac{n}{\frac{1}{x_1}+\dots+\frac{1}{x_n}}=\frac{n}{\sum_{i=1}^n \frac{1}{x_i}} \\ \\ \\ \]
\[ \text{Quadratic Mean}=\sqrt{\frac{x_1^2+\dots+x_n^2}{n}}=\sqrt{\frac{\sum_{i=1}^n x_i^2}{n}} \]
This HM-GM-AM-QM inequality is a fundamental result in mathematic involving the harmonic mean, geometric mean, arithmetic mean, and the quadratic mean:
Consider \(x_1, x_2, \dots, x_n\) as positive real numbers. The following inequality, known as the HM-GM-AM-QM inequality, holds:
\[ 0 \lt \frac{n}{\sum_{i=1}^n \frac{1}{x_i}} \le \underbrace{\sqrt[n]{\prod_{i=1}^n x_i} \le \frac{\sum_{i=1}^n x_i}{n}}_{\text{AM-GM Inequality}} \le \sqrt{\frac{\sum_{i=1}^n x_i^2}{n}} \]
Equality holds if \( x_1 = x_2 = \dots = x_n \).
If \(n=2\), the inequality becomes:
\[ 0 \lt \frac{2x_1x_2}{x_1+x_2} \le \sqrt{x_1x_2} \le \frac{x_1+x_2}{2} \le \sqrt{\frac{x_1^2+x_2^2}{2}} \]
If \(n=3\), the inequality becomes:
\[ 0 \lt \frac{3x_1x_2x_3}{x_1x_2+x_2x_3+x_3x_1} \le \sqrt[3]{x_1x_2x_3} \le \frac{x_1+x_2+x_3}{3} \le \sqrt{\frac{x_1^2+x_2^2+x_3^2}{3}} \]
We can now solve several new problems using the relationships we’ve just established. The identities we’ve encountered remain useful, and the ‘grouping’ technique continues to be applicable.
Let \(a,b,c\) be positive real numbers, and \(abc=1\). Without using the AM-GM inequality prove that:
\[ab+bc+ca\ge3\]
Hint 1
Consider applying the HM-GM inequality.
Solution
Using the HM-GM inequality, we know:
\[ \begin{cases} \frac{3*abc}{ab+bc+ca} \le \sqrt[3]{abc} \\ abc=1 \end{cases} \Rightarrow 3 \le ab+bc+ca \]
Equality holds when \(a=b=c=1\).
Let \(a,b,c,x,y,z\) be positive real numbers such that \(x+y+z=a+b+c=1\). Prove that:
\[ \frac{1}{ax+by+cz}+\frac{1}{cx+ay+bz}+\frac{1}{bx+cy+az} \ge 9 \]
Hint 1
Can the HM-AM inequality help in solving this problem?
Solution
We apply the HM-AM inequality in the following manner:
\[ \frac{\sum\frac{1}{ax+by+cz}}{3} \ge \frac{3}{(ax+by+cz)+(cx+ay+bz)+(bx+cy+az)} \Leftrightarrow \\ \sum\frac{1}{ax+by+cz} \ge \frac{9}{a(x+y+z)+b(x+y+z)+c(x+y+z)} \Leftrightarrow \\ \sum\frac{1}{ax+by+cz} \ge \frac{9}{(a+b+c)(x+y+z)} \Leftrightarrow \\ \sum\frac{1}{ax+by+cz} \ge 9 \]
When does the equality holds?
In a similar fashion with the previous problem let’s try to solve the next inequality:
Let \(x,y,z\) positive real numbers such that \(x+y+z=k\), \(k\) fixed. Prove that:
\[ \frac{1}{\sqrt{xy+yz}}+\frac{1}{\sqrt{yz+zx}}+\frac{1}{\sqrt{zx+xy}} \geq \frac{6}{k} \]
Hint 1
Can the AM-HM inequality help in solving this problem?
Hint 2
Can you prove that:
\[ \sqrt{xy+yz} \leq \frac{k}{2} \]
Solution
We apply the AM-HM inequality:
\[ \frac{\frac{1}{\sqrt{xy+yz}}+\frac{1}{\sqrt{yz+zx}}+\frac{1}{\sqrt{zx+xy}}}{3} \geq \frac{3}{\sqrt{xy+yz}+\sqrt{yz+zx}+\sqrt{zx+xy}} = \] \[ = \frac{3}{\sqrt{y(x+z)}+\sqrt{z(x+y)}+\sqrt{x(y+z)}} = \] \[ = \frac{3}{\sqrt{y(k-y)}+\sqrt{z(k-z)}+\sqrt{x(k-x)}} \]
Therefore:
\[ \frac{1}{\sqrt{xy+yz}}+\frac{1}{\sqrt{yz+zx}}+\frac{1}{\sqrt{zx+xy}} \geq \] \[ \geq \frac{9}{\sqrt{y(k-y)}+\sqrt{z(k-z)}+\sqrt{x(k-x)}} \tag{1} \]
We observe that for any term from the denominator we can apply the AM-GM in the following manner:
\[ \sqrt{a(k-a)} \leq \frac{a+k-a}{2} = \frac{k}{2} \]
Using this in \((1)\) proves our inequality:
\[ \frac{9}{\sqrt{y(k-y)}+\sqrt{z(k-z)}+\sqrt{x(k-x)}} \geq \frac{9}{\frac{k}{2}+\frac{k}{2}+\frac{k}{2}} = \frac{6}{k} \]
Let \(a,b,c \in \mathbb{R}^*_{+}\) such that \(abc=1\), prove that:
\[ \sum_{\text{cyc}} \frac{5+\frac{a+b}{c}+\frac{b+c}{a}}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}} \leq 3 + 2*\sum_{\text{cyc}}a \]
Hint 1
Recall that \(abc=1\) often provides powerful simplifications. First, observe that:
\[ \frac{3}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}} \leq 3\sqrt[3]{abc} = 1 \]
Hint 2
Since \(abc=1\) try rewriting each fraction in a more uniform way:
\[ \frac{1}{a}+\frac{1}{b}+\frac{1}{c} = \frac{bc+ac+ab}{abc} = bc+ac+ab \]
Solution
\(abc=1\) is my favorite condition.
Since \(abc=1\):
\[ \begin{align} \frac{1}{a}+\frac{1}{b}+\frac{1}{c} = \frac{bc+ac+ab}{abc} = bc+ac+ab \tag{1} \end{align} \] \[ \begin{align} \frac{3}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}} = \frac{3abc}{ab+bc+ca} = \frac{3}{ab+bc+ca} \leq 3\sqrt[3]{abc} = 1 \tag{2} \end{align} \]
From (1) and \(c=\frac{1}{ab}, a=\frac{1}{bc}\):
\[ S = \sum_{\text{cyc}} \frac{5+\frac{a+b}{c}+\frac{b+c}{a}}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}} = \sum_{\text{cyc}}\frac{5+ab(a+b)+bc(b+c)}{ab+bc+ca} = \] \[ = \sum_{\text{cyc}} \frac{3}{ab+bc+ca} + \sum_{\text{cyc}} \frac{2+ab(a+b)+bc(b+c)}{ab+bc+ca} = \] \[ = \sum_{\text{cyc}} \frac{3}{ab+bc+ca} + \sum_{\text{cyc}} \frac{ab^2+a^2b + abc + bc^2+b^2c+abc}{ab+bc+ca} = \] \[ = \sum_{\text{cyc}} \frac{3}{ab+bc+ca} + \sum_{\text{cyc}} \frac{b(ab+bc+ca)+c(ab+bc+ca)}{ab+bc+ca} = \] \[ = \sum_{\text{cyc}} \frac{3}{ab+bc+ca} + \sum_{\text{cyc}} \frac{(b+c)(ab+bc+ca)}{ab+bc+ca} = \] \[ = \sum_{\text{cyc}} \frac{3abc}{ab+bc+ca} + \sum_{\text{cyc}}(b+c) = \] \[ = \sum_{\text{cyc}} \frac{3abc}{ab+bc+ca} + 2\sum_{\text{cyc}}a \]
Since \(\sum_{\text{cyc}} \frac{3abc}{ab+bc+ca} \leq 3\) then:
\[ S \leq 3 + 2\sum_{\text{cyc}}a = 3 + 2(a+b+c) \]
Source
Andrei N. Ciobanu
Let \(a,b,c\) positive real numbers such that \(abc=1\). Prove the inequality:
\[ \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c} \leq \frac{a^2+b^2+c^2}{2} \]
Hint 1
Solution
First, observe that:
\[ \begin{align} \frac{a^2+b^2+c^2}{2} \geq \frac{ab+bc+ca}{2} \tag{1} \end{align} \]
Since \( abc = 1 \), we have:
\[ \begin{align} \frac{1}{a}+\frac{1}{b}+\frac{1}{c} = \frac{ab+bc+ca}{abc} = ab+bc+ca \end{align} \]
Combining (1) and (2), we obtain:
\[ \frac{a^2+b^2+c^2}{2} \geq \frac{1}{2} \left(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\right) \]
Therefore, to prove the original inequality, it suffices to show that:
\[ \begin{align} \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a} \leq \frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \tag{3} \end{align} \]
To prove this, we apply the Harmonic Mean-Arithmetic Mean (HM-AM) inequality:
\[ \frac{a+b}{2} \geq \frac{2}{\frac{1}{a}+\frac{1}{b}} \Leftrightarrow \frac{1}{a+b} \leq \frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}\right) \] \[ \frac{c+a}{2} \geq \frac{2}{\frac{1}{c}+\frac{1}{a}} \Leftrightarrow \frac{1}{c+a} \leq \frac{1}{4}\left(\frac{1}{c}+\frac{1}{a}\right) \] \[ \frac{b+c}{2} \geq \frac{2}{\frac{1}{b}+\frac{1}{c}} \Leftrightarrow \frac{1}{b+c} \leq \frac{1}{4}\left(\frac{1}{b}+\frac{1}{c}\right) \]
Summing all three inequalities proves inequality \((3)\), and thus the original statement.
Source
Romanian Math Olympiad, Etapa Locala, 8th grade, Galati, 2014
Let \(a,b,c \in (0,1)\) or \(a,b,c \in (1, \infty)\). Prove that:
\[ \log_a bc + \log_b ca + \log_c ab \ge 4\left( \log_{ab} c +\log_{bc} a + \log_{ca} b\right) \]
Hint 1
Perform a base change for each logarithm to express all terms in terms of a common logarithm.
Solution
In problems involving logarithmic inequalities, it is often useful to express all logarithms using a common base. Let \( k \neq 1 \) be an arbitrary positive base. Using the base change formula:
\[ \log_x y = \frac{\log_k y}{\log_k x}, \]
, we rewrite the given inequality:
\[ \frac{\log_k b + \log c}{\log_k a}+\frac{\log_k c + \log_k a}{\log_k b} + \frac{\log_k a + \log_k b}{\log_k c} \ge \\ \frac{4\log_k c}{\log_k a + \log_k b} + \frac{4\log_k a}{\log_k b + \log_k c}+\frac{4\log_k b}{\log_k a + \log_k c} \]
Introducing the notation:
\[ x = \log_k a, \quad y = \log_k b, \quad z = \log_k c \]
we reformulate the inequality as:
\[ \frac{y+z}{x} + \frac{z+x}{y} + \frac{x+y}{z} \overbrace{\ge}^{?} \frac{4x}{y+z} + \frac{4y}{z+x} + \frac{4z}{x+y} \]
Rewriting each fraction, we obtain:
\[ \left(\frac{x}{y}+\frac{x}{z}\right) + \left(\frac{y}{x}+\frac{y}{z}\right) + \left(\frac{z}{x}+\frac{z}{y}\right) \overbrace{\ge}^{?} \frac{4x}{y+z} + \frac{4y}{z+x} + \frac{4z}{x+y} \]
To establish this inequality, we apply the AM-HM (Arithmetic Mean - Harmonic Mean) inequality:
\[ \frac{\frac{x}{y}+\frac{x}{z}}{2} \ge \frac{2}{\frac{y}{x}+\frac{z}{x}} \Leftrightarrow \frac{x}{y} + \frac{x}{z} \ge \frac{4x}{y+z}, \\ \frac{\frac{y}{x}+\frac{y}{z}}{2} \ge \frac{2}{\frac{x}{y}+\frac{z}{y}} \Leftrightarrow \frac{y}{x} + \frac{y}{z} \ge \frac{4y}{x+z}, \\ \frac{\frac{z}{x}+\frac{z}{y}}{2} \ge \frac{2}{\frac{x}{z}+\frac{y}{z}} \Leftrightarrow \frac{z}{x} + \frac{z}{y} \ge \frac{4z}{x+y} \]
Summing these three inequalities gives the desired result:
\[ \frac{x}{y} + \frac{x}{z} + \frac{y}{x} + \frac{y}{z} + \frac{z}{x} + \frac{z}{y} \geq \frac{4x}{y+z} + \frac{4y}{x+z} + \frac{4z}{x+y}. \]
Thus, the original inequality is proved.
When does equality hold?
Source
Romanian Math Olympiad, 2006 (?)
Find \(x,y,z \in \mathbb{R}_{+}\) if:
\[ \begin{cases} x^3 + 3 \le 4z \\ y^3 + 3 \le 4x \\ z^3 + 3 \le 4z \end{cases} \]
Hint 1
Try giving values to \(x, y, z\) to find a solution.
Hint 2
Can you prove that:
\[ x^4y^4z^4\ge(4x-3)(4y-3)(4z-3) \]
Hint 3
Can you prove that:
\[x^4y^4z^4\le(4x-3)(4y-3)(4z-3)\]
Solution
Intuitively, we observe that \(x = y = z = 1\) is a solution. But are there more solutions?
\[ \begin{cases} x^3y + 3 \le 4z \\ y^3z + 3 \le 4x \\ z^3x + 3 \le 4y \\ \end{cases} \Leftrightarrow \begin{cases} x^3y \le 4z - 3 \\ y^3z \le 4x - 3 \\ z^3x \le 4y - 3 \\ \end{cases} \]
Since \(x, y, z \in \mathbb{R}_{+}\), we can multiply all three inequalities to obtain::
\[ (xyz)^4 \le (4x-3)(4y-3)(4z-3) \]
On the other hand, applying the mean inequality chain:
\[ \begin{cases} x^4 + 1 \ge 2x^2 \Rightarrow x^4+3 \ge 2(x^2+1) \ge 4x \Rightarrow x^4 \ge 4x - 3\\ y^4 + 1 \ge 2y^2 \Rightarrow y^4+3 \ge 2(y^2+1) \ge 4y \Rightarrow y^4 \ge 4y - 3 \\ z^4 + 1 \ge 2z^2 \Rightarrow z^4+3 \ge 2(z^2+1) \ge 4z \Rightarrow z^4 \ge 4z - 3 \\ \end{cases} \]
Multiplying the last relationships:
\[(xyz)^4 \ge (4x-3)(4y-3)(4z-3)\]
So on one hand we have: \((xyz)^4 \le (4x-3)(4y-3)(4z-3)\) and on the other: \((xyz)^4 \ge (4x-3)(4y-3)(4z-3)\).
Therefore, we can conclude that \(x=y=z=1\) is the unique solution satisfying both inequalities.
Source
The Romanian Math Olympiad
The weighted AM-GM inequality
The Weighted AM-GM inequality is a generalization of the standard AM-GM inequality that includes weights for each term.
Let \(a_1, a_2, \dots, a_n\) positive real numbers, and their associated (positive real) weights \(w_1, w_2, \dots, w_n\), such that:
\[ w_1 + w_2 + \dots + w_n = W \]
The Weighted AM-GM inequality states:
\[ \frac{a_1w_1+a_2w_2+\dots+a_nw_n}{W} \ge (a_1^{w_1}a_2^{w_2}\dots a_n^{w_n})^{\frac{1}{W}} \]
If \(W=1\), the inequality has the following form:
\[ a_1w_1+a_2w_2+\dots+a_nw_n \ge a_1^{w_1}a_2^{w_2}\dots a_n^{w_n} \]
If \(w_1=w_2=\dots=w_n=1\) then \(W=n\), so we obtain the "classical" AM-GM inequality:
\[ \frac{a_1+a_2+\dots+a_n}{n} \ge (a_1a_2\dots a_n)^{\frac{1}{n}} \]
Let’s try a classical exercise:
If \(a,b\) real positive numbers, if \(p>1\) and \(q>1\) are real numbers such that: \(\frac{1}{p}+\frac{1}{q} = 1\), prove:
\[ qa^p+pb^q \ge qab + pba \]
Hint 1
Given that \(\frac{1}{p} + \frac{1}{q} = 1\), it follows that \(p + q = pq\).
Solution
Using the fact that \(p + q = pq\), we can rewrite the inequality as:
\[ qa^p+pb^q \ge qab + pba \Leftrightarrow qa^p + pb^q \ge ab(\underbrace{p+q}_{=pq}) \Leftrightarrow \\ \Leftrightarrow a^p * \frac{1}{p} + b^q * \frac{1}{q} \ge ab \]
Next, apply the Weighted AM-GM inequality with the weights \(w_1 = \frac{1}{p}\) and \(w_2 = \frac{1}{q}\), where \(W = w_1 + w_2 = 1\):
\[ \frac{a^p * \frac{1}{p} + b^q * \frac{1}{q}}{\frac{1}{p}+\frac{1}{q}} \ge [(a^p)^{\frac{1}{p}}*(b^q)^{\frac{1}{q}}]^{\frac{1}{\frac{1}{p}+\frac{1}{q}}} \Leftrightarrow \\ \Leftrightarrow a^p * \frac{1}{p} + b^q * \frac{1}{q} \ge ab \]
Source
This exercise is a reformulation of Young's Inequality for products, which is itself a consequence of the more general Weighted AM-GM inequality.
Now, let’s try to solve a classical problem proposed by Nguyen Manh Dung (I’ve found it in multiple sources) using the Weighted AM-GM inequality:
Let \(a,b,c\) positive real numbers such that \(a+b+c=1\). Prove that:
\[ a^ab^bc^c + a^bb^cc^a + a^cb^ac^b \le 1 \]
Hint 1
\(W=a+b+c=1\)
Solution
We permute the weights in the following manner (keeping in mind \(W=a+b+c=1\)):
\[ \begin{cases} \frac{\textbf{a}*a + \textbf{b}*b + \textbf{c}*c}{\textbf{a}+\textbf{b}+\textbf{c}} \ge a^ab^bc^c \\ \frac{\textbf{b}*a + \textbf{c}*b + \textbf{a}*c}{\textbf{b}+\textbf{c}+\textbf{a}} \ge a^bb^cc^a \\ \frac{\textbf{c}*a + \textbf{a}*b + \textbf{b}*c}{\textbf{b}+\textbf{c}+\textbf{a}} \ge a^cb^ac^b \\ \end{cases} \Leftrightarrow \begin{cases} a^2+b^2+c^2 \ge a^ab^bc^c \\ ba + cb + ac \ge a^bb^cc^a \\ ca + ab + bc \ge a^cb^ac^b \end{cases} \]
By summing the three:
\[ (a^2+b^2+c^2) + 2(ab+bc+ca) = (a+b+c)^2 = 1 \ge a^ab^bc^c + a^bb^cc^a + a^cb^ac^b \]
Source
Nguyen Manh Dung
The last problem in this section is authored by Dan Sitaru, the editor of the Romanian Mathematical Magazine:
Let \(a,b,c,d>0\), prove that:
\[ (a+c)^c(b+d)^d(c+d)^{c+d} \le c^dd^d(a+b+c+d)^{c+d} \]
Hint 1
Group the terms by their powers.
Hint 2
By "regrouping the terms", the new inequality becomes:
\[ \frac{(a+c)^c}{c^c} * \frac{(b+d)^d}{d^d} \le \frac{(a+b+c+d)^{c+d}}{(c+d)^{c+d}} \]
Solution
By "regrouping the terms" based on their corresponding powers, the inequality is equivalent to:
\[ \Bigl( \frac{a+b+c+d}{c+d} \Bigl)^{c+d} \ge \Bigl( \frac{a}{c}+1 \Bigl)^c \Bigl( \frac{b}{d} + 1 \Bigl)^d \]
In the same time if we apply the Weighted AM-GM inequality to \( \Bigl(\frac{a}{c}+1 \Bigl), \Bigl( \frac{b}{d} + 1\Bigl)\), with the weights \(w_1=c\) and \(w_2=d\), we would obtain:
\[ \frac{c*(\frac{a}{c}+1) + d*(\frac{b}{d}+1)}{c+d} \ge \Bigl[\Bigl(\frac{a}{c}+1\Bigl)^c\Bigl(\frac{b}{d}+1\Bigl)^d\Bigl]^{\frac{1}{c+d}} \Leftrightarrow \\ \frac{a+b+c+d}{c+d} \ge \Bigl[\Bigl(\frac{a}{c}+1\Bigl)^c\Bigl(\frac{b}{d}+1\Bigl)^d\Bigl]^{\frac{1}{c+d}} \]
After raising each side at \(c+d\):
\[ \Bigl( \frac{a+b+c+d}{c+d} \Bigl)^{c+d} \ge \Bigl(\frac{a}{c}+1\Bigl)^c\Bigl(\frac{b}{d}+1\Bigl)^d \]
Source
Dan Sitaru
The power of substitutions
Actually, there’s no real power in substitutions; it’s simply that our brains are inept at handling “complications”.
Substitutions are powerful mechanisms in mathematics because they simplify complex problems, reveal hidden structures, and transform seemingly impossible problems into more familiar or solvable forms. By changing variables, substitutions allow viewing the same problem from different perspectives, often leading to new insights - or new problems. I assure you, problem creators love substitutions.
In this regard, let’s solve the following inequality:
Let \(x,y,z\) positive real numbers suchat that \(xyz=1\). Prove the following inequality:
\[ \frac{1+xy}{1+z}+\frac{1+yz}{1+x}+\frac{1+zx}{1+y} \geq 3 \]
Hint 1
When the condition \( xyz = 1 \) appears, a powerful strategy is to perform the substitution (homogenisation):
\[ x = \frac{a}{b}, \quad y = \frac{b}{c}, \quad z = \frac{c}{a} \]
This substitution preserves the condition \( xyz = \frac{a}{b} \cdot \frac{b}{c} \cdot \frac{c}{a} = 1 \).
Solution
Apply the substitution:
\[ x = \frac{a}{b}, \quad y = \frac{b}{c}, \quad z = \frac{c}{a} \]
Then the inequality becomes:
\[ \frac{1+\frac{a}{b}\cdot\frac{b}{c}}{1+\frac{c}{a}} + \frac{1+\frac{b}{c}\cdot\frac{c}{a}}{1+\frac{a}{b}}+\frac{1+\frac{c}{a}\cdot\frac{a}{b}}{1+\frac{b}{c}} \geq 3 \Leftrightarrow \]
Simplify each term:
\[ \frac{a}{c}+\frac{c}{b}+\frac{b}{a} \overbrace{\geq}^{?} 3 \]
By the AM-GM inequality the last inequality is true:
\[ \frac{a}{c}+\frac{c}{b}+\frac{b}{a} \geq 3\cdot\sqrt[3]{\frac{a}{c}\cdot\frac{c}{b}\cdot\frac{b}{a}} = 3 \]
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Arges, 2012
Or inequation:
Solve for \(x \in \mathbb{R}\):
\[ E(x) = 18^x + 12^x + 9^x + 4^x + 3^x + 2^x \leq 6^{x+1} \]
Hint 1
Before jumping into direct manipulations, see if you can transform or "bound" the left-hand side \(E(x)\) by recognizing common factors or applying a well-known inequality such as AM-GM.
If you can show \(E(x)\) is both \(\geq\) "some value" and \(\leq\) that "same value", you could then solve \(E(x) = \text{(that value)}\) instead of tackling the full inequality from scratch.
Hint 2
It might help to divide every term by \(6^x\).
Hint 3
Consider substituting some terms.
Solution
Intuition: observe that each base on the left \((18, 12, 9, 4, 3, 2)\) is a product of prime factors \(2\) and \(3\). A natural step is to factor out \(6^x\) from both sides.
We divide by \(6^x=(2\cdot3)^x\) both sides:
\[ E(x) = 3^x+2^x+\left(\frac{3}{2}\right)^x + \left(\frac{2}{3}\right)^x + \left(\frac{1}{3}\right)^x + \left(\frac{1}{2}\right)^x \leq 6 \]
Next, let:
\[ a \rightarrow 3^x, \quad b \rightarrow 2^x, \quad c \rightarrow 1 \]
Then the left hand side expression becomes:
\[ E(x) = \frac{a}{b} + \frac{b}{a} + \frac{a}{c} + \frac{c}{a} + \frac{b}{c} + \frac{c}{b} \]
Using the AM-GM inequality, each pair \(\frac{a}{b}, \frac{b}{a}\) is \(\geq2\):
\[ E(x) = \sum_{\text{cyc}}\left(\underbrace{\frac{a}{b}+\frac{b}{a}}_{\geq2}\right) \geq 6 \]
But from our rearranged inequality, we also have \(E(x) \le 6\). Hence \(E(x)\) must equal 6 exactly, which forces each pair to satisfy equality in AM-GM. That happens if and only if:
\[ 6 \leq E(x) \leq 6 \Rightarrow a=b=c \Rightarrow 3^x = 2^x = 1 \Rightarrow x = 0 \]
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Satu-Mare, 2013 (Galambosi Csaba)
Or this equation:
Find all real triplets \((a,b,c)\) satisfying:
\[ (2^{2a}+1)\cdot(2^{2b}+2)\cdot(2^{2c}+8)=2^{a+b+c+5} \]
Hint 1
To simplify things, introduce some substitutions. Notice that each term on the left is of the form \(2^{2x}\) plus a constant, and the right side has a power of 2. Try setting \(x = 2^a\), \(y = 2^b\), \(z = 2^c\).
Hint 2
After you rewrite the equation via substitutions, see if you can prove that the left-hand side is at least \(2^{a+b+c+5}\).
Solution
Rewrite the equation with a helpful substitution:
\[ x=2^{2a}, \quad y=2^{2b}, \quad z=2^{2c} \]
Substituting into the original equation gives:
\[ (x^2+1)(y^2+2)(z^2+2^3)=32xyz \]
Use the AM-GM inequality on each factor:
\[ x^2+1\geq 2x, \quad y^2+2 \geq 2y\sqrt{2}, \quad z^2+2^3 \geq 4z\sqrt{2} \]
When we multiply these three inequalities together:
\[ (x^2+1)(y^2+2)(z^2+2^3) \geq 32xyz \]
Excellent! for the equation to hold, all the individual AM-GM steps must be equalities, so \(x^2=1\), \(y^2=2\) and \(z^2=2^3\).
We have found \((a,b,c)\) = \((0, \frac{1}{2}, \frac{3}{2})\).
Source
Hong-Kong Team Selection Test, 2021
Radicals can be nasty to handle. If you can isolate them and make a clever substitution, go for it, don’t hesitate!
Let \(x, y, z\) be positive real numbers. Prove that:
\[ 3 \ge \frac{2(\sqrt{x}+1)}{2(\sqrt{x}+1)+x} + \frac{2(\sqrt{y}+1)}{2(\sqrt{y}+1)+y} + \frac{2(\sqrt{z}+1)}{2(\sqrt{z}+1)+z} \]
Hint 1
Rewrite the fractions in terms of perfect squares:
\[\frac{2(\sqrt{x}+1)}{2(\sqrt{x}+1)+x}=\frac{2(\sqrt{x}+1)}{(\sqrt{x}+1)^2+1}\]
Solution
Using the hint, we rewrite each term in the sum:
\[ \frac{2(\sqrt{x}+1)}{2(\sqrt{x}+1)+x} = \frac{2(\sqrt{x}+1)}{(\sqrt{x}+1)^2+1}. \]
Thus, the inequality to prove becomes:
\[ 3 \geq \frac{2(\sqrt{x}+1)}{(\sqrt{x}+1)^2+1} + \frac{2(\sqrt{y}+1)}{(\sqrt{y}+1)^2+1} + \frac{2(\sqrt{z}+1)}{(\sqrt{z}+1)^2+1}. \]
Introduce the substitution:
\[ \begin{cases} a = \sqrt{x} + 1, \\ b = \sqrt{y} + 1, \\ c = \sqrt{z} + 1. \end{cases} \]
Rewriting the terms using this notation:
\[ 3 \geq \frac{2}{a + \frac{1}{a}} + \frac{2}{b + \frac{1}{b}} + \frac{2}{c + \frac{1}{c}}. \]
By AM-GM, we have:
\[ a + \frac{1}{a} \geq 2, \quad b + \frac{1}{b} \geq 2, \quad c + \frac{1}{c} \geq 2. \]
Thus, applying this bound to each fraction:
\[ \frac{2}{a + \frac{1}{a}} + \frac{2}{b + \frac{1}{b}} + \frac{2}{c + \frac{1}{c}} \leq \frac{2}{2} + \frac{2}{2} + \frac{2}{2} = 3. \]
This completes the proof.
Equality holds when \(a=b=c=1\).
Source
Andrei N. Ciobanu
As a general piece of advice, whenever you encounter logarithms in an inequality, you can try two approaches: either make a clever substitution or rewrite everything in a common base. Let’s apply this idea to the next problem:
Let \(a,b,c \in (0,1)\). Prove the following inequality:
\[ \frac{1}{2+\log_a b} + \frac{1}{2+\log_b c} + \frac{1}{2+\log_c b} \leq 1 \]
Hint 1
A key observation is the well-known identity:
\[ \log_a b \cdot \log_b c \cdot \log_c a = \frac{\ln b}{\ln a} \cdot \frac{\ln c}{\ln b} \cdot \frac{\ln a}{\ln c} = 1 \]
Solution
First, define:
\[ \log_a b \rightarrow x, \quad \log_b c \rightarrow y, \quad \log_c b \rightarrow z \]
With these substitutions, and noting \(\log_a b \cdot \log_b c \cdot \log_c a = 1\) implying \(xyz=1\), the original inequality becomes:
\[ \frac{1}{2+x}+\frac{1}{2+y}+\frac{1}{2+z} \leq 1 \]
A common tactic is to clear denominators and compare sums of products:
\[ (2+x)(2+y)+(2+y)(2+z)+(2+z)(2+x) \leq \] \[ \leq (2+x)(2+y)(2+z) \Leftrightarrow \] \[ 4+2y+2x+xy + 4+2z+2y+yz + 4+2x+2z+zx \leq \] \[ \leq 8+4(x+y+z)+2(xy+xz+yz)+xyz \Leftrightarrow \] \[ 12 + 4(x+y+z)+(xy+yz+zx) \leq \] \[ \leq 8+4(x+y+z)+2(xy+xz+yz)+\underbrace{xyz}_{=1} \Leftrightarrow \] \[ xy+yz+zx \geq 3 \]
At this point we simply apply the AM-GM inequality:
\[ \frac{xy+yz+zx}{3} \geq 3\sqrt[3]{x^2y^2z^2} = 3 \]
Equality holds when \(x = y = z\), or equivalently \(\log_a b = \log_b c = \log_c b\), leading to \(a=b=c\). This completes the proof.
Source
Romanian Math Olympiad, Etapa Locala, 10th grade, Bihor, 2013
Ravi Substitutions
A special type of substitution, known as Ravi Substitution, is a powerful technique used in geometric inequalities involving the sides of a triangle. The key idea is to express the sides of the triangle in terms of sums of positive variables, which often simplifies the given inequality and makes algebraic manipulations more natural. This transformation is particularly useful when dealing with symmetric inequalities in triangle geometry.
This technique gets its name from Ravi Vakil a mathematician known for his contributions to algebraic geometry. The technique appears in mathematical problem-solving, particularly in inequalities involving the sides of a triangle. He wasn’t the first one to introduce it (it appears in books of problems prior to 1940), but he was the one to popularise it.
In its most basic form, Ravi substitution works as follows:
Let \(a,b,c\) be the sides of a triangle. The triangle inequality states that:
\[ a+b \gt c, \quad b+c \gt a, \quad c+a\gt b \]
To handle this structure more easily, we introduce new "variables":
\[ a = x + y, \quad b = y+z, \quad c = z+x \]
Where \(x,y,z\) are positive real numbers.
Why is Ravi substition useful ?
First of all, it eliminates the triangle constraints. In a triangle with sides \(a,b,c\) the triangle inequality states that \(a+b \gt c\), \(b+c \gt a\), and \(c+a \gt b\). By setting \(a=x+y\), \(b=y+z\), and \(c=z+x\), these inequalities automatically hold, and its no longer needed to explicitly verify them. For example:
\[ a+b \gt c \Leftrightarrow \underbrace{(x+y)}_{a} + \underbrace{(y+z)}_{b} \gt \underbrace{z+x}_{c} \Leftrightarrow (z+x)+2y \gt z+x \Leftrightarrow 2y \gt 0 \]
With this new technique in mind, let’s try solving the following IMO problems:
Let \(a,b,c\) be the lengths of a triangle, show that:
\[ a^2(b+c-a) + b^2(c+a-b) + c^2(a+b-c) \leq 3abc \]
Solution
Using Ravi's substitution, introduce positive real number \(x,y,z\) such that:
\[ a = x+y, \quad b = y+z, \quad c=z+x \]
Substituting these expressions into the given inequality, we rewrite it as:
\[ (x+y)^2(y+z+z+x-x-y) + (y+z)^2(z+x+x+y-y-z)+ \\ (z+x)^2(x+y+y+z-z-x) \leq 3(x+y)(y+z)(z+x) \Leftrightarrow \\ \]
After expansion and simplification, the inequality reduces to:
\[ (x^2y+y^2z+z^2x+xy^2)+(xy^2+yz^2+zx^2) \overbrace{\ge}^{?} 6xyz \]
Applying the AM-GM inequality separately to each group::
\[ x^2y+y^2z+z^2x \ge 3\sqrt[3]{(xyz)^3} = 3xyz \\ xy^2+yz^2+zx^2 \ge 3\sqrt[3]{(xyz)^3} = 3xyz \]
Adding both inequalities proves the initial inequality:
\[ (\underbrace{x^2y+y^2z+z^2x+xy^2}_{\geq 3xyz})+(\underbrace{xy^2+yz^2+zx^2}_{\geq 3xyz}) \ge 6xyz \]
When does the equality hold? Is the triangle equilateral?
Source
IMO 1964
Let \(a,b,c\) be the lengths of the sides of a triangle. Prove the inequality:
\[ a^2b(a-b)+b^2c(b-c)+c^2a(c-a) \geq 0 \]
Solution
Using Ravi substition, and after expanding and simplifying, the inequality becomes:
\[ xy^3 + yz^3 + zx^3 \geq xyz(x+y+z) \]
We apply the AM-GM inequality to establish:
\[ \begin{cases} x^3z+xy^2z \ge 2x^2yz \\ xy^3+xyz^2 \ge 2xy^2z \\ yz^3+x^2yz \ge 2xyz^3 \end{cases} \]
Adding these inequalities together gives:
\[ (x^3z+xy^3+yz^3) + xyz(x+y+z) \ge 2xyz(x+y+z) \Leftrightarrow \\ x^3z+xy^3+yz^3 \ge xyz(x+y+z) \]
This confirms the given inequality.
When does equality hold?
Source
IMO 1983
Nesbitt’s Inequality
Nesbitt’s Inequality is a classic and elegant result in inequalities, commonly taught in competitive mathematics. Using it can help you bypass tedious steps where you would otherwise need to apply AM-GM or other inequalities.
I was curious to learn more about Nesbitt, but there is little information about him online. Eventually, I came across this link.
In a generalized form:
If \(x_1, x_2, \dots, x_n\) are positive real numbers, and \(S=\sum_{i=1}^n x_i\), then:
\[\sum_{i=1}^n \frac{a_i}{S-a_i}\ge\frac{n}{n-1} \]
Equality holds if \(x_1=x_2=\dots=x_n\).
Most of the times you will apply it in this form:
If \(a,b,c\) are positive positive real numbers, then:
\[ \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b} \ge \frac{3}{2} \]
Can you prove Nesbitt’s inequality using known inequalities (AM-HM, I am looking at you!)?
Let \(x_1, x_2, \dots, x_n\) be positive real numbers, and \(S=\sum_{i=1}^n x_i\), prove:
\[ \sum_{i=1}^n \frac{a_i}{S-a_i}\ge\frac{n}{n-1} \]
Note
The proof using the AM-HM inequality might feel a bit counterintuitive. However, there are simpler approaches using other inequalities, which we will explore in later sections.
Hint 1
The AM-HM inequality states that:
\[ \frac{\sum_{i=1}^n a_i}{n} \geq \frac{n}{\sum_{i=1}^n \frac{1}{a_i}} \]
Solution
We start by rewriting the given sum:
\[ \sum_{i=1}^n \left(\frac{a_i}{s-a_i}\right) = \sum_{i=1}^n \left( \frac{S}{S-a_i} - 1 \right) = \]
Factoring \(S\):
\[ = S \sum_{i=1}^n \left( \frac{1}{S-a_i} \right) - n \]
Now, we apply AM-HM to the denominator:
\[ \frac{n}{\sum_{i=1}^n \left( \frac{1}{S-a_i} \right)} \leq \frac{\sum_{i=1}^n\left(S-a_i\right)}{n} = S - \frac{S}{n} = S \left(\frac{n-1}{n}\right) \]
Rearranging this inequality:
\[ \sum_{i=1}^n \left(\frac{1}{S-a_i}\right) \ge \frac{n^2}{S(n-1)} \]
Substituting this into our earlier expression \(\sum_{i=1}^n \left(\frac{a_i}{s-a_i}\right)=S \sum_{i=1}^n \left( \frac{1}{S-a_i} \right) - n\) gives us:
\[ \sum_{i=1}^n \frac{a_i}{S-a_i} \ge \frac{Sn^2}{S(n-1)} - n = \frac{n}{n-1} \]
Thus, the inequality is proven.
Can you solve the next problems using substitutions and Nesbitt’s Inequality ?
Let \( x,y,z \in (1,\infty) \). Prove that:
\[ \log_{xy}z+\log_{yz}x+\log_{zx}y\ge\frac{3}{2} \]
Hint 1
Consider applying a change of base to each logarithmic term. This is a common theme in problems involving logarithms and inequalities.
Hint 2
After the change of base, we have the following:
\[ \log_{xy} z = \frac{\log_n z}{\log_n{xy}} \]
Solution
First, apply the change of base formula to each logarithmic expression:
\[ \begin{cases} \log_{xy}z=\frac{\log_{n}z}{\log_n{xy}}=\frac{\log_{n}z}{\log_{n}x+\log_{n}y} \\ \log_{yz}x=\frac{\log_{n}x}{\log_n{yz}}=\frac{\log_{n}x}{\log_{n}y+\log_{n}z} \\ \log_{zx}y=\frac{\log_{n}y}{\log_n{zx}}=\frac{\log_{n}y}{\log_{n}z+\log_{n}x} \end{cases} \]
Next, substitute \( a = \log_n x \), \( b = \log_n y \), and \( c = \log_n z \). This transforms the inequality into:
\[ \frac{a}{b+c} + \frac{b}{a+c} + \frac{c}{a+b} \ge \frac{3}{2}, \]
Which is a direct application of Nesbitt's inequality.
Equality holds true if \(x=y=z\).
Let \(x, y, z\) be positive real numbers. Prove the following inequality:
\[ \frac{zy}{x(z+y)}+\frac{zx}{y(z+x)}+\frac{xy}{z(x+y)} \ge \frac{3}{2} \]
Solution
We apply a substitution to Nesbitt's inequality. Let:
\[ a \rightarrow \frac{1}{x}, \quad b \rightarrow \frac{1}{y}, \quad c \rightarrow \frac{1}{z}. \]
This transforms Nesbitt's inequality into:
\[ \frac{\frac{1}{x}}{\frac{1}{y} + \frac{1}{z}} + \frac{\frac{1}{y}}{\frac{1}{x} + \frac{1}{z}} + \frac{\frac{1}{z}}{\frac{1}{x} + \frac{1}{y}} \ge \frac{3}{2}. \]
Simplifying, we obtain:
\[ \frac{yz}{x(y+z)} + \frac{xz}{y(x+z)} + \frac{xy}{z(x+y)} \ge \frac{3}{2}. \]
Therefore, the inequality is proven. Equality holds if \(x = y = z\).
For the next one, there’s an easy solution using the AM-GM inequality, but can you prove it using Nesbitt’s inequality instead?
Let \(x, y, z \in \mathbb{R}_{+}\) be the sides of a triangle. Prove that:
\[ \frac{-x+y+z}{x}+\frac{x-y+z}{y}+\frac{x+y-z}{z} \ge 3 \]
Hint 1
Divide each term by 2:
\[ \frac{-x + y + z}{2x} + \frac{x - y + z}{2y} + \frac{x + y - z}{2z} \geq \frac{3}{2} \]
Hint 2
Consider the following substitutions:
\[ \begin{cases} a \rightarrow -x + y + z \\ b \rightarrow x - y + z \\ c \rightarrow x + y - z \end{cases} \]
Solution
After dividing each term by 2, we obtain the following inequality:
\[ \frac{-x+y+z}{2x}+\frac{x-y+z}{2y}+\frac{x+y-z}{2z} \ge \frac{3}{2} \]
We then perform the substitutions:
\( \begin{cases} a \rightarrow -x+y+z \\ b \rightarrow x-y+z \\ c \rightarrow x+y-z \end{cases} \)
Since \(x, y, z\) are the sides of a triangle, we know the following relations hold:
\[ \begin{cases} a \rightarrow -x+y+z \gt 0 \\ b \rightarrow x-y+z \gt 0 \\ c \rightarrow x+y-z \gt 0 \end{cases} \]
We observe the following relations:
\[ \begin{cases} a+b \rightarrow 2z \\ b+c \rightarrow 2x \\ c+a \rightarrow 2y \\ \end{cases} \]
Thus, the inequality becomes:
\[ \sum \frac{-x+y+z}{(x-y+z)+(x+y-z)} \ge \frac{3}{2} \Leftrightarrow \\ \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b} \overbrace{\ge}^{Nesb.} \frac{3}{2} \]
Equality holds if \(x=y=z\).
Source
Andrei N. Ciobanu
Can you solve the next problems using Nesbitt’s Inequality:
Let \(a,b,c\) be positive real numbers such that \(a+b+c=1\). Prove the inequality:
\[ \frac{1+a}{1-a}+\frac{1+b}{1-b}+\frac{1+c}{1-c} \ge 6 \]
Hint 1
Note that if \(a + b + c = 1\), then \(1 - a = b + c\), and similarly for \(b\) and \(c\).
Solution
Using the given condition \(a + b + c = 1\), we rewrite:
\[ 1 - a = b + c, \quad 1 - b = a + c, \quad 1 - c = a + b. \]
Similarly, we express the numerators:
\[ 1 + a = 2a + b + c, \quad 1 + b = 2b + a + c, \quad 1 + c = 2c + a + b. \]
Substituting these into the given expression:
\[ \frac{1 + a}{1 - a} + \frac{1 + b}{1 - b} + \frac{1 + c}{1 - c} = \frac{2a + b + c}{b + c} + \frac{2b + a + c}{a + c} + \frac{2c + a + b}{a + b}. \]
Simplifying each fraction:
\[ \frac{2a + b + c}{b + c} = 1 + \frac{a}{b + c}, \quad \frac{2b + a + c}{a + c} = 1 + \frac{b}{a + c}, \quad \frac{2c + a + b}{a + b} = 1 + \frac{c}{a + b}. \]
Thus, the inequality reduces to:
\[ 1 + \frac{a}{b + c} + 1 + \frac{b}{a + c} + 1 + \frac{c}{a + b} \ge 6. \]
Rearranging:
\[ \frac{a}{b + c} + \frac{b}{a + c} + \frac{c}{a + b} \ge \frac{3}{2}. \]
This follows directly from Nesbitt's inequality.
Let \(a,b,c\) positve real numbers. Prove that:
\[ \frac{a^2+1}{b+c}+\frac{b^2+1}{c+a}+\frac{c^2+1}{a+b} \ge 3 \]
Hint 1
The \(3\) is missing the \(\frac{1}{2}\).
Solution
First, apply the inequality \(a^2 + 1 \geq 2a\) (by AM-GM) to each numerator:
\[ \frac{\overbrace{a^2 + 1}^{\geq 2a}}{b+c} + \frac{\overbrace{b^2 + 1}^{\geq 2b}}{c+a} + \frac{\overbrace{c^2 + 1}^{\geq 2c}}{a+b} \geq \frac{2a}{b+c} + \frac{2b}{c+a} + \frac{2c}{a+b} \]
Now, divide each term by 2:
\[ \frac{a}{b+c} + \frac{b}{c+a} + \frac{c}{a+b} \overbrace{\geq}^{Nesb.} \frac{3}{2} \Leftrightarrow \\ \]
Thus, we have proven the inequality. Equality holds when \(a = b = c = 1\).
Let \(a, b, c\) be positive real numbers such that \(a+b+c = 3\). Prove that:
\[ \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a} \ge \frac{3}{2} \]
Hint 1
We can rewrite each fraction as:
\[ \frac{1}{a+b}=\frac{a+b+c}{(a+b)(a+b+c)} \]
Solution
We begin by rewriting the left-hand side of the inequality:
\[ \frac{1}{a+b} + \frac{1}{b+c} + \frac{1}{c+a} = \sum \frac{(a+b) + c}{(a+b)(a+b+c)} = \]
We can simplify the sum as follows:
\[ = \frac{1}{a+b+c} \left( \frac{c}{a+b} + \frac{a}{b+c} + \frac{b}{c+a} + \frac{a+b}{a+b} + \frac{b+c}{b+c} + \frac{c+a}{c+a} \right) = \\ = \frac{1}{3} \left( \frac{c}{a+b} + \frac{a}{b+c} + \frac{b}{c+a} + 3 \right) \]
Notice that the last three terms simplify to 3, and by Nesbitt's inequality, we have:
\[ \frac{c}{a+b} + \frac{a}{b+c} + \frac{b}{c+a} \geq \frac{3}{2} \]
Thus, we get:
\[ \frac{1}{a+b} + \frac{1}{b+c} + \frac{1}{c+a} \geq \frac{1}{3} \left( \frac{3}{2} + 3 \right) = \frac{3}{2} \]
The equality holds when \(a = b = c = 1\).
The next one looks rather peculiar, but can you solve it using Nesbitt’s Inequality and something else ?
Let \(x,y,z\) be positive real numbers, prove that:
\[ \frac{2^{x-y+1}}{1+2^{z-y}}+\frac{2^{y-z+1}}{1+2^{x-z}}+\frac{2^{z-x+1}}{1+2^{y-x}}\ge\frac{2x}{1+x^2}+\frac{2y}{1+y^2}+\frac{2z}{1+z^2} \]
Hint 1
Can you isolate the right-hand side from the left-hand side?
Hint 2
Can you apply Nesbitt's inequality to the left-hand side by making appropriate substitutions?
Hint 3
Can you show that the right-hand side is less than or equal to \(3\)?
Solution
We begin by examining the right-hand side, which can be rewritten as:
\[ R=\frac{2x}{1+x^2}+\frac{2y}{1+y^2}+\frac{2z}{1+z^2}=\frac{2}{\frac{1}{x}+x}+\frac{2}{\frac{1}{y}+y}+\frac{2}{\frac{1}{z}+z} \]
Applying the Harmonic Mean-Geometric Mean (HM-GM) inequality, we get:
\[ \begin{cases} \frac{2}{\frac{1}{x}+x} \le \sqrt{\frac{1}{x}*x} = 1\\ \frac{2}{\frac{1}{y}+y} \le \sqrt{\frac{1}{y}*y} = 1\\ \frac{2}{\frac{1}{z}+z} \le \sqrt{\frac{1}{z}*z} = 1 \end{cases} \]
This implies that:
\[ R \le \underbrace{\sqrt{\frac{1}{x}*x}}_{=1} + \underbrace{\sqrt{\frac{1}{y}*y}}_{=1} + \underbrace{\sqrt{\frac{1}{z}*z}}_{=1} \le 3 \]
Now, let's work on the left-hand side:
\[ L=\frac{2^{x-y+1}}{1+2^{z-y}}+\frac{2^{y-z+1}}{1+2^{x-z}}+\frac{2^{z-x+1}}{1+2^{y-x}}= \\ = 2[\frac{2^x}{2^y(1+2^{z-y})}+\frac{2^y}{2^z(1+2^{x-z})}+\frac{2^z}{2^x(1+2^{y-x})}] = \\ = 2(\underbrace{\frac{2^x}{2^y+2^z}+\frac{2^x}{2^y+2^z}+\frac{2^z}{2^x+2^y}}_{\ge \frac{3}{2}}) \]
Thus, we conclude that \(L \ge 3\).
Since \(L \ge 3 \) and \(3 \ge R \), we have \(L \ge R \).
The equality holds for \(x=y=z=1\).
Source
Andrei N. Ciobanu
For the next problems, the Nesbitt structure is harder to spot:
Let \(x, y, z\) be positive real numbers such that \(xyz = 1\). Prove that:
\[ \frac{1}{yz+z}+\frac{1}{zx+y}+\frac{1}{xy+z}\ge\frac{3}{2} \]
Hint 1
Since \(xyz = 1\), consider the following substitution:
\[ \begin{cases} x = \frac{a}{b} \\ y = \frac{b}{c} \\ z = \frac{c}{a} \end{cases} \]
Solution
Since \(xyz = 1\), we apply the substitution:
\[ \begin{cases} x = \frac{a}{b} \\ y = \frac{b}{c} \\ z = \frac{c}{a} \end{cases} \]
After performing the substitution, the inequality becomes:
\[ \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \overbrace{\ge}^{Nesb.} \frac{3}{2} \]
The equality holds when \(a = b = c = 1\) or equivalently when \(x = y = z = 1\).
Source
Kazakhstan Olympiad, 2008
Let \(a,b,c\) positive real numbers. Prove that:
\[ \frac{(a^3+1)^2}{4bc(b+c)}+\frac{(b^3+1)^2}{4ca(c+a)}+\frac{(c^3+1)^2}{4ab(a+b)} \ge \frac{3}{2} \]
Hint 1
In a previous exercise we've proven that:
\[ a^3+b^3 \ge ab(a+b) \]
Hint 2
Try proving the following inequality:
\[ (a+b)^2 \ge 4ab \]
Solution
Using the two hints, we can rewrite the inequality as:
\[ S = \frac{\overbrace{(a^3+1)^2}^{\ge 4a^3}}{\underbrace{4bc(b+c)}_{\le 4(b^3+c^3)}}+\frac{\overbrace{(b^3+1)^2}^{\ge 4b^3}}{\underbrace{4ca(c+a)}_{\le 4(c^3+a^3)}}+\frac{\overbrace{(c^3+1)^2}^{\ge 4c^3}}{\underbrace{4ab(a+b)}_{\le 4(a^3+b^3)}} \]
Thus, we obtain:
\[ S \ge \frac{a^3}{b^3+c^3} + \frac{b^3}{c^3+a^3} + \frac{c^3}{a^3+b^3} \overbrace{\ge}^{\text{Nesb.}} \frac{3}{2} \]
The equality holds when \(a=b=c=1\).
Source
Andrei N. Ciobanu
Let \(a,b,c\) positive real numbers. Prove that:
\[ \frac{1}{a^3+b^3+2abc}+\frac{1}{b^3+c^3+2abc}+\frac{1}{c^3+a^3+2abc} \le \frac{3}{4abc} \]
Hint 1
Can you use the following inequality:
\[a^3+b^3 \ge ab(a+b)\]
Solution
Using the fact that \(a^3 + b^3 \ge ab(a+b)\), we can rewrite the inequality as:
\[ \frac{1}{a^3+b^3+2abc}+\frac{1}{b^3+c^3+2abc}+\frac{1}{c^3+a^3+2abc} \le \\ \le \frac{1}{ab(a+b)+2abc} + \frac{1}{bc(b+c)+2abc} + \frac{1}{ca(c+a)+2abc} \]
Now, we need to prove the following inequality:
\[ \frac{1}{ab(a+b)+2abc} + \frac{1}{bc(b+c)+2abc} + \frac{1}{ca(c+a)+2abc} \overbrace{\le}^{?} \frac{3}{4abc} \Leftrightarrow \\ \frac{2c}{a+b+2c} + \frac{2a}{b+c+2a} + \frac{2b}{c+a+2b} \overbrace{\le}^{?} \frac{3}{2} \Leftrightarrow \\ 1 - \frac{a+b}{a+b+2c} + 1 - \frac{b+c}{b+c+2a} + 1 - \frac{c+a}{c+a+2b} \overbrace{\le}^{?} \frac{3}{2} \Leftrightarrow \\ \frac{(a+b)}{(a+c)+(b+c)} + \frac{(b+c)}{(b+a)+(c+a)} + \frac{(c+a)}{(c+b)+(a+b)} \overbrace{\ge}^{?} \frac{3}{2} \]
This inequality is a direct application of Nesbitt's Inequality.
The equality holds for \(a=b=c\).
Source
Stanescu Florin, Concursul Gazeta Matematica si ViitoriOlimpici, Editia a Va, 9th grade, Romania
Let \(a, b, c > -\frac{1}{2}\) be real numbers. Prove that the following inequality holds:
\[ \frac{a^2+2}{b+c+1}+\frac{b^2+2}{a+c+1}+\frac{c^2+2}{a+b+1} \geq 3 \]
Hint 1
We can attempt to "reduce" the inequality to a Nesbitt-type structure using some clever manipulations:
\[ a^2+2 = (a^2+1)+1 \geq 2a + 1 \]
But wait — can we apply the AM-GM inequality when numbers are negative? The answer is nuanced. In this particular form, the inequality remains valid. Try checking what happens when \(a\) is negative but still greater than \(-\frac{1}{2}\).
Solution
After applying the first hint, we obtain:
\[ \frac{a^2+2}{b+c+1}+\frac{b^2+2}{a+c+1}+\frac{c^2+2}{a+b+1} \geq \] \[ \geq \frac{2a+1}{b+c+1} + \frac{2b+1}{a+c+1}+\frac{2c+1}{a+b+1} \tag{1} \]
Since \(a, b, c > -\frac{1}{2}\), it is natural to make a substitution that eliminates the complications arising from possible negative values. Set:
\[ x = a+\frac{1}{2}, \quad y = b+\frac{1}{2}, \quad z=c+\frac{1}{2} \]
Thus, equivalently:
\[ a = x-\frac{1}{2}, \quad b = y-\frac{1}{2}, \quad c=z-\frac{1}{2} \]
Substituting into \((1)\), the expression becomes:
\[ \frac{2a+1}{b+c+1} + \frac{2b+1}{a+c+1}+\frac{2c+1}{a+b+1} = 2\cdot\sum_{\text{cyc}} \frac{x}{y+z} \geq 3 \]
This leads us directly to Nesbitt's inequality, thus completing the proof.
Source
Marian Ionescu, Shortlisted for the Romanian Olympiad 2007
The final problem presents a fascinating inequality that resembles Nesbitt’s Inequality structure, though not exactly. Nevertheless, it’s an interesting and noteworthy result:
Let \(x,y,z\) positive real numbers, with \(x+y+z=3\), prove that:
\[ \frac{\sqrt{x}}{y+z}+\frac{\sqrt{y}}{x+z}+\frac{\sqrt{z}}{y+x} \ge \frac{3}{2} \]
Hint 1
Maybe it's worth performing a substition like:
\[ \begin{cases} x = a^2 \\ y = b^2 \\ z = c^2 \end{cases} \]
In this case, the additional condition becomes:
\[ a^2+b^2+c^2=3 \]
Solution
The solution was provided by Michael Rozenberg on math.stackexchange.com
We start by performing the following substition:
\[ \begin{cases} x = a^2 \\ y = b^2 \\ z = c^2 \end{cases} \]
After the substition, the inequality becomes:
\( (\frac{a}{3-a^2}-1)+(\frac{b}{3-b^2}-1)+(\frac{c}{3-c^2}-1) \ge 0 \Leftrightarrow \\ \frac{1}{2}[\frac{(a-1)(a+3)}{3-b^2}+\frac{(b-1)(b+3)}{3-b^2}+\frac{(c-1)(c+3)}{3-c^2}] \ge 0 \Leftrightarrow \\ \frac{1}{2}[\frac{(a-1)(a+3)}{3-b^2}+\frac{(b-1)(b+3)}{3-b^2}+\frac{(c-1)(c+3)}{3-c^2} - (a^2-1) - (b^2-1) - (c^2-1)] \ge 0 \Leftrightarrow \\ \frac{1}{2}[\frac{(a-1)^2(a+2)a}{3-a^2}+\frac{(b-1)^2(b+2)b}{3-b^2}+\frac{(c-1)^2(c+2)c}{3-c^2}] \ge 0 \)
The last inequality is true, because each of the three terms is positive.
Equality holds for \(x=y=z=1\).
Source
The Cauchy-Bunyakovsky-Schwartz Inequality
Together with the AM-GM inequality, the CBS Inequality forms the cornerstone of inequality problems in intermediate and advanced math competitions. In its simplest algebraic form, it appears as follows:
For the real numbers \(a_{i=1 \dots n}, b_{i=1 \dots n}\) the inequality states:
\[ \Bigl(\sum_{i=1}^n a_i b_i\Bigl)^2 \le \Bigl(\sum_{i=1}^n a_i^2\Bigl)\Bigl(\sum_{i=1}^n b_i^2\Bigl) \]
Equality holds if \(a_i = k*b_i\), \(\forall i\).
Alternatively, in expanded form:
You would be surprised in how many ways the CBS Inequality can be applied.
Can you solve the next problems using the CBS Inequality ?
Let \(a,b,c\) real numbers. Show that:
\[ 3(a^2+b^2+c^2)\ge(a+b+c)^2 \]
Hint 1
Consider expressing \(3\) as \(1^2 + 1^2 + 1^2\).
Solution
By writing \(3 = 1^2 + 1^2 + 1^2\), the following relationship holds by the CBS Inequality:
\[(1^2+1^2+1^2)(a^2+b^2+c^2)\ge(a*1+b*1+c*1)^2\]
The equality holds when \(a = b = c\).
Let \(x, y, z \in \mathbb{R}\). Prove that:
\[ 3x^2+10y^2+15z^2 \ge 2(x+y+z)^2 \]
Hint 1
Notice that:
\[ \frac{1}{3} + \frac{1}{10} + \frac{1}{15} = \frac{1}{2} \]
Solution
We use \(\left( \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{10}}, \frac{1}{\sqrt{15}} \right)\) and \(\left( x \sqrt{3}, y \sqrt{10}, z \sqrt{15} \right)\), and apply the CBS Inequality:
\[ \left( \underbrace{\frac{1}{3} + \frac{1}{10} + \frac{1}{15}}_{\frac{1}{2}} \right) (3x^2 + 10y^2 + 15z^2) \ge \left( \frac{x \sqrt{3}}{\sqrt{3}} + \frac{y \sqrt{10}}{\sqrt{10}} + \frac{z \sqrt{15}}{\sqrt{15}} \right)^2 \] \[ \Rightarrow (3x^2 + 10y^2 + 15z^2) \ge 2(x + y + z)^2 \]
When does the equality hold?
Let \(n\in\mathbb{N}\), prove that:
\[ \frac{n^2}{(n+1)^2}\le\sum_{i=1}^n\frac{1}{i^2}*\sum_{i=2}^{n+1}\frac{1}{i^2} \]
Solution
Expanding the sums, the right-hand side (RHS) becomes:
\[ R=\sum_{i=1}^n\frac{1}{i^2}*\sum_{i=2}^{n+1}\frac{1}{i^2} = (1+\frac{1}{2^2}+\dots+\frac{1}{n^2})(\frac{1}{2^2}+\dots+\frac{1}{(n+1)^2}) \]
By applying the CBS (Cauchy-Bunyakovsky-Schwarz) inequality, we know that:
\[ (\frac{1}{1*2}+\frac{1}{2*3}+\dots+\frac{1}{n(n+1)})^2 \le R \Leftrightarrow \\ (1-\frac{1}{n+1})^2 \le R \Leftrightarrow \\ (\frac{n}{n+1})^2 \le R \]
When does the equality hold?
Let \(a, b, c\) be positive real numbers such that \(a + b + c = 3\). Prove that:
\[ a^2+b^2+c^2 \ge 3 \ge ab + bc + ca \]
Note
We already know that \(a^2 + b^2 + c^2 \ge ab + bc + ca\), but this alone is insufficient to prove the full chain inequality.
Hint 1
It might seem trivial, but recall that \(3 = 1 + 1 + 1\).
Hint 2
Consider applying the Cauchy-Bunyakovsky-Schwarz (CBS) inequality with \((1, 1, 1)\) and \((a^2, b^2, c^2)\).
Solution
We apply the CBS inequality as follows:
\[ (1^2+1^2+1^2)(a^2+b^2+c^2) \ge (a+b+c)^2 \Leftrightarrow \\ 3(a^2+b^2+c^2) \ge 9 \Leftrightarrow \\ a^2+b^2+c^2 \ge 3 \]
Next, we prove that \(3 \ge ab + bc + ca\).
We use the identity:
\[ a^2+b^2+c^2 = (a+b+c)^2 - 2(ab+bc+ca) \ge 3 \Leftrightarrow \\ 9 - 2(ab+bc+ca) \ge 3 \Leftrightarrow 6 \ge 2(ab+bc+ca) \Leftrightarrow 3 \ge ab+bc+ca \]
When doest equality hold ?
Let \(a, b, c, d, e \in \mathbb{R}\) with \(a^2 + b^2 + c^2 + d^2 + e^2 = 55\). Prove that:
\[a+2b+3c+4d+5e \le 55\]
Hint 1
Note that \(1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 1 + 4 + 9 + 16 + 25 = 55\).
Solution
We apply the Cauchy-Bunyakovsky-Schwarz (CBS) inequality as follows:
\[ (1^2+2^2+3^2+4^2+5^2)(a^2+b^2+c^2+d^2+e^2) \ge (a+2b+3c+4d+5e)^2 \Leftrightarrow \\ 55 * 55 \ge (a+2b+3c+4d+5e)^2 \Leftrightarrow \\ 55 \ge |a+2b+3c+4d+5e| \ge a+2b+3c+4d+5e \]
When does the equality hold?
We have already proven the following inequality (as part of a previous problem) using the AM-GM inequality. However, can you find a solution that uses the Cauchy-Schwarz inequality instead?
Let \(x,y,z\) positive real numbers. Prove the inequality:
\[ xy^3+yz^3+zx^3 \ge xyz(x+y+z) \]
Note
As a reminder, proving the inequality using the AM-GM inequality involves the grouping of terms:
\[ x^3z + xy^2z \geq 2x^2yz \\ xy^3 + xyz^2 \geq 2xy^2z \\ yz^3 + x^2yz \geq 2xyz^2 \]
The inequality is proven by summing the three relationships.
Solution
We can solve this exercise in "one go" by applying the CBS inequality as follows:
\[ (x^3z + xy^3 + yz^3)(z+x+y) \ge (y\sqrt{xyz}+z\sqrt{xyz}+x\sqrt{xyz})^2 \Leftrightarrow \\ x^3z + xy^3 + yz^3 \ge \frac{xyz(x+y+z)^2}{x+y+z} = xyz(x+y+z) \]
Let \(a, b\) be positive real numbers satisfying \(a + b = 1\). Prove that:
\[\sqrt{1+2a}+\sqrt{1+2b}\le 2\sqrt{2}\]
Solution
We apply the Cauchy-Bunyakovsky-Schwarz (CBS) inequality as follows:
\[ (1*\sqrt{1+2a}+1*\sqrt{1+2b})^2 \le (1^2+1^2)(1+2a+1+2b) \]
Eventually \[\sqrt{1+2a}+\sqrt{1+2b}\le2\sqrt{2}\]
Source
Problem author: Ioan V. Maftei, Bucharest, Romania, Concursul Gazeta Matematica, 9th grade
Let \(a,b,c\) positive real numbers, prove the inequality:
\[ \sqrt{a(b+c)}+\sqrt{b(c+a)}+\sqrt{c(a+b)} \leq \sqrt{2}(a+b+c) \]
Solution
Applying the CBS inequality in the following manner and keeping in mind that \(a,b,c\) are positive numbers:
\[ \left(\sqrt{a(b+c)}+\sqrt{b(c+a)}+\sqrt{c(a+b)}\right)^2 \overbrace{\leq}^{\text{CBS}} \] \[ \leq (a+b+c)((b+c)+(c+a)+(a+b)) \Leftrightarrow \] \[ \sqrt{a(b+c)}+\sqrt{b(c+a)}+\sqrt{c(a+b)} \leq \sqrt{(a+b+c)(2a+2b+2c)} = \] \[ = \sqrt{2}(a+b+c) \]
It's important to notice that equality holds when: \(\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}\).
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Brasov, 2014
Let \(x, y, z \in (0, \infty)\) and \(x+y+z=6\). Prove that:
\[ x\sqrt{x-1}+y\sqrt{y-1}+z\sqrt{z-1} \ge 6 \]
Hint 1
Try to find a simple but effective substitution.
Hint 2
Perform the following substitutions to simplify the inequality:
\[ \begin{cases} \sqrt{x-1}=a \\ \sqrt{y-1}=b \\ \sqrt{z-1}=c \end{cases} \]
Solution
There are multiple solutions to this problem, but one effective approach uses the Cauchy-Bunyakovsky-Schwarz (CBS) inequality.
We start by performing the substitutions:
\[ \begin{cases} \sqrt{x-1}=a \\ \sqrt{y-1}=b \\ \sqrt{z-1}=c \end{cases} \Leftrightarrow \begin{cases} x=a^2+1 \\ y=b^2+1 \\ z=c^2+1 \end{cases} \]
The constraint for \(a, b, c\) is now \(x + y + z = (a^2 + b^2 + c^2) + 3 \Rightarrow a^2 + b^2 + c^2 = 3\).
The inequality becomes:
\[ a(a^2+1)+b(b^2+1)+c(c^2+1) \ge 6 \Leftrightarrow \\ \Leftrightarrow (a^3+b^3+c^3)+(a+b+c) \ge 6 \]
Now, apply the AM-GM inequality and then the CBS inequality:
\[ (a^3+b^3+c^3)+(a+b+c) \overbrace{\ge}^{AM-GM} 2 \sqrt{(a^3+b^3+c^3)(a+b+c)} \\ \overbrace{\ge}^{CBS} 2\sqrt{(a^2+b^2+c^2)^2} \ge 6 \]
Equality holds when \(x=y=z=2\) or \(a=b=c=1\).
Source
Craciun Gheorghe
Let \(x,y,z \ge 1\) such that \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=2\). Prove the inequality:
\[ \sqrt{x+y+z} \ge \sqrt{x-1} + \sqrt{y-1} + \sqrt{z-1} \]
Hint 1
From the given condition, attempt to obtain a new expression involving \(x-1\), \(y-1\) and \(z-1\).
Solution
We begin by manipulating the given condition:
\[ \left(1-\frac{1}{x}\right)+\left(1-\frac{1}{y}\right) + \left(1-\frac{1}{z}\right) \ge 3-2 \Leftrightarrow \] \[ \frac{x-1}{x} + \frac{y-1}{y} + \frac{z-1}{z} = 1 \]
Now, apply the Cauchy-Schwarz inequality (CBS inequality) in the form:
\[ (x+y+z)(\frac{x-1}{x} + \frac{y-1}{y} + \frac{z-1}{z}) \overbrace{\ge}^{CBS} \] \[ \ge (\sqrt{x-1}+\sqrt{y-1}+\sqrt{z-1})^2 \]
Which, after taking the square root of both sides, simplifies to:
\[ \sqrt{x+y+z} \ge \sqrt{x-1}+\sqrt{y-1}+\sqrt{z-1} \]
Source
Iran, 1998
Let \(a, b, c\) be positive real numbers such that \(a^2 + b^2 + c^2 = 1\). Prove that:
\(a^3+b^3+c^3 \ge \frac{\sqrt{3}}{3}\)
Hint 1
Can you relate \(a^3 + b^3 + c^3\) to \(a^2 + b^2 + c^2\) and \(a + b + c\) by applying the Cauchy-Bunyakovsky-Schwarz (CBS) inequality twice?
Solution
We aim to connect \(a^3 + b^3 + c^3\) to the given condition \(a^2 + b^2 + c^2 = 1\). Let's start with an application of the CBS inequality:
\[ \left[\left(\sqrt{a}\right)^2+\left(\sqrt{b}\right)^2+\left(\sqrt{c}\right)^2\right]*\left[\left(a\sqrt{a}\right)^2+\left(b\sqrt{b}\right)^2+\left(c\sqrt{c}\right)^2\right] \geq \] \[ \geq \left(\sqrt{a}*a\sqrt{a}+\sqrt{b}*b\sqrt{b}+\sqrt{c}*c\sqrt{c}\right)^2 \Leftrightarrow \] \[ \left(a+b+c\right)\left(a^3+b^3+c^3\right) \geq \left(a^2+b^2+c^2\right)^2 \Leftrightarrow \] \[ \left(a+b+c\right)\left(a^3+b^3+c^3\right) \geq 1 \]
Now let's connect \(a+b+c\) and \(a^2+b^2+c^2\) through the CBS inequality:
\( (1^2+1^2+1^2)(a^2+b^2+c^2)\ge(a*1+b*1+c*1)^2 \Leftrightarrow 3 \ge (a+b+c)^2 \Leftrightarrow \sqrt{3} \ge a+b+c \)
At this point, we can write:
\( \sqrt{3}*(a^3+b^3+c^3) \ge (a+b+c)*(a^3+b^3+c^3) \ge 1 \Rightarrow \\ \Rightarrow a^3+b^3+c^3 \ge \frac{\sqrt{3}}{3} \)
When does the equality hold?
We’ve already proven Nesbitt’s Inequality using the AM-GM inequality, but can you prove it using the CBS Inequality? In case you need help, please follow the generous hints.
Let \(a, b, c\) be positive real numbers. Prove Nesbitt's Inequality using the CBS Inequality:
\[ \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b} \ge \frac{3}{2} \]
Hint 1
Try proving an equivalent inequality:
\[ \frac{a}{b+c} + 1 + \frac{b}{a+c} + 1 + \frac{c}{a+b} + 1 \ge \frac{9}{2} \]
Solution
We begin by adding \(3\) to both sides of the inequality we aim to prove:
\[ \frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1\ge\frac{9}{2} \]
This leads to the equivalent inequality:
\[ \frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1 \overbrace{\ge}^{?} \frac{9}{2} \Leftrightarrow \\ \frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{c+a} \overbrace{\ge}^{?} \frac{9}{2} \Leftrightarrow \\ (a+b+c)(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}) \overbrace{\ge}^{?} \frac{9}{2} \Leftrightarrow \\ \frac{2}{2}(a+b+c)(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}) \overbrace{\ge}^{?} \frac{9}{2} \Leftrightarrow \\ [(a+b)+(b+c)+(c+a)](\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}) \overbrace{\ge}^{CBS} 9 \\ \]
The last inequality is true as a direct consequence of the CBS inequality.
The equality holds for \(a=b=c=1\).
The following problem uses an interesting pattern/trick, can you solve it ?
Let \(a\), \(b\), and \(c\) be positive real numbers satisfying \(a^2 + b^2 + c^2 \ge 4\). Prove that:
\[ \frac{a^3}{b+3c}+\frac{b^3}{c+3a}+\frac{a^3}{a+3b}\ge1 \]
Hint 1
How can you use the CBS inequality to make the condition \(a^2 + b^2 + c^2 \ge 4\) more relevant?
Hint 2
If \(a_1\), \(a_2\), \(a_3\) and \(b_1\), \(b_2\), \(b_3\) are positive real numbers, can you prove the following useful inequality?
\[ a_1+a_2+a_3 \ge \frac{\sqrt{a_1b_1}+\sqrt{a_2b_2}+\sqrt{a_3b_3}}{b_1+b_2+b_3} \]
Solution
How can use the fact that \(a^2+b^2+c^2\ge4\)?
For \(a_1, a_2, a_3, b_1, b_2, b_3\) positive numbers, a direct consequence of the CBS inequality is:
\[ (\sqrt{a_1}*\sqrt{b_1}+\sqrt{a_2}\sqrt{b_2}+\sqrt{a_3}\sqrt{b_3})^2 \le (a_1+a_2+a_3)(b_1+b_2+b_3) \Leftrightarrow \\ a_1 + a_2 + a_3 \ge \frac{(\sqrt{a_1b_1}+\sqrt{a_2b_2}+\sqrt{a_3b_3})^2}{b_1+b_2+b_3} \]
The trick is to choose \(b_1, b_2, b_3\) in such a way that they simplify our inequality. Let:
\[ \begin{cases} a_1 \rightarrow \frac{a^3}{b+3c} \\ a_2 \rightarrow \frac{a^3}{c+3a} \\ a_3 \rightarrow \frac{c^3}{a+3b} \\ b_1 \rightarrow a(b+3c) \\ b_2 \rightarrow b(c+3a) \\ b_3 \rightarrow c(a+3b) \\ \end{cases} \]
By applying this substitution to the left-hand side of the inequality:
\[ \sum \frac{a^3}{b+3c} \ge \frac{\left[\sqrt{\frac{a^3}{b+3c}*a(b+3c)}+\sqrt{\frac{b^3}{c+3a}*b(c+3a)}+\sqrt{\frac{c^3}{a+3b}*c(a+3b)}\right]^2}{a(b+3c)+b(c+3a)+c(a+3b)} = \]
After simplifying:
\[ = \frac{(a^2+b^2+c^2)^2}{4(ab+bc+ca)} = \frac{a^2+b^2+c^2}{4} * \frac{a^2+b^2+c^2}{ab+bc+ca} \ge 1 \]
We've already proven that \(a^2+b^2+c^2 \ge ab+bc+ca\), and we know that \(a^2+b^2+c^2 \ge 4\) so the inequality is true.
Source
Concursul Gazeta Matematica, Editia a IXa, 9th grade, Romania
Let \(\lambda \ge 3\) be fixed, and let \(x\), \(y\), and \(z\) be positive real numbers such that \(x + y + z = 3\). Find the minimum of:
\[ P = \frac{x}{\lambda - x}+\frac{y}{\lambda - y} + \frac{z}{\lambda - z} \]
Hint 1
If \(a_1\), \(a_2\), and \(a_3\), as well as \(b_1\), \(b_2\), and \(b_3\), are positive real numbers, can you prove the following useful inequality?
\[ a_1+a_2+a_3 \ge \frac{\sqrt{a_1b_1}+\sqrt{a_2b_2}+\sqrt{a_3b_3}}{b_1+b_2+b_3} \]
Solution
We can apply the CBS inequality in the following way:
\[ [\frac{x}{\lambda - x}+\frac{y}{\lambda - y} + \frac{z}{\lambda - z}][x(\lambda-x)+y(\lambda-y)+z(\lambda-z)] \ge (x+y+z)^2 \]
This simplifies to:
\[ \frac{x}{\lambda - x}+\frac{y}{\lambda - y} + \frac{z}{\lambda - z} \ge \frac{9}{\lambda(x+y+z)-(x^2+y^2+z^2)} \Leftrightarrow \\ \frac{x}{\lambda - x}+\frac{y}{\lambda - y} + \frac{z}{\lambda - z} \ge \frac{9}{3\lambda - (x^2+y^2+z^2)} \]
Now, we need to find a lower bound for \(x^2 + y^2 + z^2\), given that \(x + y + z = 3\). To do this, we apply the CBS inequality again:
\[ (x^2+y^2+z^2)(1^2+1^2+1^2)\ge(x+y+z)^2 \Leftrightarrow \\ x^2+y^2+z^2 \ge 3 \]
Using this, our previous inequality becomes:
\[ \frac{x}{\lambda - x}+\frac{y}{\lambda - y} + \frac{z}{\lambda - z} \ge \frac{9}{3\lambda - (x^2+y^2+z^2)} \Leftrightarrow \\ \frac{x}{\lambda - x}+\frac{y}{\lambda - y} + \frac{z}{\lambda - z} \ge \frac{9}{3\lambda-3} = \frac{3}{\lambda-1} \]
Therefore, we have \(P \ge \frac{3}{\lambda - 1}\). Equality holds when \(x = y = z = 1\).
Source
Mariciu Chiriciu
Let \(z \in [0, \infty)\), and \(x, y \in [1, \infty)\). Prove the following inequality:
\[ \frac{x+y}{(y+z)(z+x)}+xyz \ge \frac{x+y+z}{xy+yz+zx} \]
Hint 1
Do you notice any similarities between the terms of this inequality and those in a known identity?
Hint 2
Can you use the following identity to your advantage? It looks suspiciously similar to our inequality, except some things might need adjustment:
\( (x+y)(y+z)(z+x)+xyz=(x+y+z)(xy+yz+zx) \)
Solution
We can apply the CBS inequality in the following manner:
\[ [\frac{x+y}{(y+z)(z+x)}+xyz][\underbrace{(x+y)(y+z)(z+x)+xyz}_{=(x+y+z)(xy+yz+zx)}]\overbrace{\ge}^{CBS}(x+y+xyz)^2 \]
Using this, we can rewrite the inequality as:
\[ \frac{x+y}{(y+z)(z+x)}+xyz \ge \frac{(x+y+\overbrace{xyz}^{\ge z})^2}{(x+y+z)(xy+yz+zx)} \ge \\ \ge \frac{(x+y+z)^2}{(x+y+z)(xy+yz+zx)} = \\ = \frac{x+y+z}{xy+yz+zx} \]
When does equality holds?
Source
Andrei N. Ciobanu
Can you think of an identity and some algebraic manipulations to solve the next problem:
Let \(x, y, z\) be positive real numbers. If:
\[ k = \frac{1}{z}(x + 2\sqrt{yz}) + \frac{1}{x}(y + 2\sqrt{zx}) + \frac{1}{y}(z + 2\sqrt{xy}), \]
Prove the following inequality:
\[ \left(1 + \frac{y}{x}\right)\left(1 + \frac{z}{y}\right)\left(1 + \frac{x}{z}\right) \ge k - 1. \]
Hint 1
Start by proving \(k \cdot xyz = (x\sqrt{y} + y\sqrt{z} + z\sqrt{x})^2\).
Hint 2
Note that: \[ \left(1 + \frac{y}{x}\right)\left(1 + \frac{z}{y}\right)\left(1 + \frac{x}{z}\right) = \frac{(x + y)(y + z)(z + x)}{xyz}. \]
Hint 3
Can you express \((x + y)(y + z)(z + x)\) using a known identity?
Solution
We start by working with \(k\) and multiplying both sides by \(xyz\):
\[ k * xyz = xy(x+2\sqrt{yz})+yz(y+2\sqrt{zx})+xz(z+2\sqrt{xy}) \Leftrightarrow \\ k * xyz = x^2y + y^2z + xz^2 + 2(xy\sqrt{yz}+yz\sqrt{zx}+2xz\sqrt{xy}) \Leftrightarrow \\ k * xyz = (x\sqrt{y}+y\sqrt{z}+z\sqrt{x})^2 \Leftrightarrow \\ k = \frac{(x\sqrt{y}+y\sqrt{z}+z\sqrt{x})^2}{xyz} \]
Now, we can rewrite the inequality as:
\[ (1+\frac{y}{x})(1+\frac{z}{y})(1+\frac{x}{z}) \ge \frac{(x\sqrt{y}+y\sqrt{z}+z\sqrt{x})^2}{xyz} - 1 \Leftrightarrow \\ \Leftrightarrow (x+y)(y+z)(z+x) \ge (x\sqrt{y}+y\sqrt{z}+z\sqrt{x})^2 - xyz \]
In the same time:
\[ (x+y)(y+z)(z+x) = (x+y+z)(xy+yz+zx) - xyz \overbrace{\ge}^{\text{C.B.S}} \\ \ge (x\sqrt{y}+y\sqrt{z}+z\sqrt{x})^2 - xyz \]
Source
Andrei N. Ciobanu
The next problem looks more difficult than it is in reality:
Let \(a,b,c\) positive real numbers, prove that:
\[ \sqrt{\frac{ab}{ab+c(a+b+c)}}+\sqrt{\frac{bc}{bc+a(a+b+c)}}+\sqrt{\frac{ca}{ca+b(a+b+c)}} \leq \frac{3}{2} \]
Hint 1
Regroup and factor the denominator of each term. In particular, observe that:
\[ \sqrt{\frac{ab}{ab+c(a+b+c)}} = \sqrt{ab} \cdot \frac{1}{\sqrt{ab+ca+cb+c^2}} = \sqrt{ab} \cdot \frac{1}{\sqrt{(a+b)(a+c)}} \]
Solution
After factoring the denominators, we can rewrite the original inequality as:
\[ \sum_{\text{cyc}} \frac{ab}{ab+c(a+b+c)} \leq \frac{3}{2} \Leftrightarrow \sum_{\text{cyc}} \left(\sqrt{ab}\cdot\frac{1}{\sqrt{(a+b)(b+c)}}\right) \leq \frac{3}{2} \]
Next, we apply the Cauchy–Bunyakovsky–Schwarz (CBS) inequality in its "reverse" form:
\[ \sum_{\text{cyc}} \left(\sqrt{ab}\cdot\frac{1}{\sqrt{(a+b)(b+c)}}\right) \leq \sqrt{\left(\sum_{cyc} ab\right)\cdot\left[\sum_{\text{cyc}}\frac{1}{(a+b)(b+c)}\right]} \]
Therefore, it suffices to prove:
\[ \sqrt{\left(\sum_{cyc} ab\right)\cdot\left[\sum_{\text{cyc}}\frac{1}{(a+b)(b+c)}\right]} \overbrace{\leq}^{?} \frac{3}{2} \Leftrightarrow \] \[ \sqrt{(ab+bc+ca)}\cdot\sqrt{\frac{1}{(a+b)(b+c)}+\frac{1}{(b+c)(c+a)}+\frac{1}{(c+a)(a+b)}} \overbrace{\leq}^{?} \frac{3}{2} \]
Squaring both sides, this becomes the more tractable condition:
\[ 8\cdot(ab+bc+ca)(a+b+c) \overbrace{\leq}^{?} 9 \cdot (a+b)(b+c)(c+a) \]
After further simplification or factorization it leads to:
\[ (ab+bc+ca)(a+b+c) \overbrace{\geq}^{?} 9\cdot abc \]
Finally, by the AM-GM inequality, \[ ab + bc + ca \;\ge\; 3\sqrt[3]{(abc)^2} \quad\text{and}\quad a + b + c \;\ge\; 3\sqrt[3]{abc}. \] Multiplying these two inequalities yields \(\,(ab+bc+ca)(a+b+c)\,\ge\,9\,abc,\) completing the proof.
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Galati, 2008
An interesting refinement for Nesbitt’s inequality
Refinement of an inequality refers to the process of strengthening or improving an existing inequality by making it sharper or more precise. This typically involves replacing a given inequality with a stronger one that still holds under the same conditions but provides a tighter bound.
I was reading an article about how Nesbitt’s inequality can be useful for solving certain geometric inequalities—particularly those involving the sides of a triangle (though we won’t be discussing that topic in this article). During my reading, I came across an interesting refinement: A new generalisation of Nesbitt’s Inequality, by D. M. Batinetu-Giurgiu and Neculai Stanciu.
Let’s try to prove it:
Let \(x, y, z, a, b\) be positive real numbers. Prove the following inequality:
\[ \frac{x}{ay+bz}+\frac{y}{ax+bz}+\frac{z}{ax+by} \ge \frac{3}{a+b} \]
Hint 1
How can you use the fact that \(a^2 + b^2 + c^2 \ge 4\)?
For positive real numbers \(a_1, a_2, a_3, b_1, b_2, b_3\), a direct consequence of the Cauchy-Schwarz inequality is:
\[ (\sqrt{a_1} \cdot \sqrt{b_1} + \sqrt{a_2} \cdot \sqrt{b_2} + \sqrt{a_3} \cdot \sqrt{b_3})^2 \le (a_1 + a_2 + a_3)(b_1 + b_2 + b_3) \\ \Rightarrow a_1 + a_2 + a_3 \ge \frac{(\sqrt{a_1b_1} + \sqrt{a_2b_2} + \sqrt{a_3b_3})^2}{b_1 + b_2 + b_3}. \]
Solution
As suggested, we apply the Cauchy-Schwarz inequality in the following manner:
\[ \frac{x}{ay + bz} + \frac{y}{ax + bz} + \frac{z}{ax + by} \ge \frac{(x + y + z)^2}{x(ay + bz) + y(ax + bz) + z(ax + by)}. \]
Now, simplify the denominator:
\[ \frac{x}{ay + bz} + \frac{y}{ax + bz} + \frac{z}{ax + by} \ge \frac{(x + y + z)^2}{a(xy + yz + zx) + b(xy + yz + zx)}. \]
Factoring out \(xy + yz + zx\) from the denominator, we obtain:
\[ \frac{x}{ay + bz} + \frac{y}{ax + bz} + \frac{z}{ax + by} \ge \frac{(x + y + z)^2}{(a + b)(xy + yz + zx)}. \]
We know that \((x + y + z)^2 \ge 3(xy + yz + zx)\), so substituting this inequality into the previous expression gives:
\[ \frac{x}{ay + bz} + \frac{y}{ax + bz} + \frac{z}{ax + by} \ge \frac{3(xy + yz + zx)}{(a + b)(xy + yz + zx)}. \]
Simplifying the right-hand side, we get:
\[ \frac{x}{ay + bz} + \frac{y}{ax + bz} + \frac{z}{ax + by} \ge \frac{3}{a + b}. \]
With this in mind, let’s try to solve the following problems:
Let \(a, b, c\) be the lengths of the sides of a triangle. Prove the following inequality:
\[ \frac{a+c-b}{a+2b-c}+\frac{a+b-c}{a+2c-b}+\frac{b+c-a}{b+2a-c} \ge \frac{3}{2} \]
Hint 1
The structure of the inequality and the presence of \( \frac{3}{2} \) on the right-hand side suggest a potential connection to the Nesbitt inequality. Can you think of useful substitutions to simplify the expression?
Hint 2
Consider using Ravi substitution, which is often helpful for triangle-related inequalities. The substitution is as follows:
\[ \begin{cases} a = x + y \\ b = y + z \\ c = z + x \end{cases} \]
Solution
After applying Ravi substitution \(a = x + y\), \(b = y + z\), and \(c = z + x\), the inequality transforms into:
\[ \frac{2x}{3y+z} + \frac{2y}{3z+x} + \frac{2z}{3x+y} \ge \frac{3}{2}. \]
This is now in a form that is similar to the Nesbitt inequality. Using the refinement for Nesbitt inequality, we obtain:
\[ \frac{x}{1.5x + 0.5y} + \frac{y}{1.5z + 0.5x} + \frac{z}{1.5x + 0.5y} \ge \frac{3}{1.5 + 0.5} = \frac{3}{2}. \]
When does the equality hold?
Source
Gheorghe Craciun, posted on the "Comunitatea Profesorilor de Matematica".
Let \(a\), \(b\), and \(c\) be positive real numbers, \(x \in (0, 6]\), and \(a + b + c = 3\). Prove the following inequality:
\[ \frac{a+1}{x(b-c)+6c}+\frac{b+1}{x(c-a)+6a}+\frac{c+1}{x(a-b)+6b} \ge 1 \]
Hint 1
Start by splitting each term on the left-hand side:
\[ \frac{a+1}{x(b-c)+6c} = \frac{a}{x(b-c)+6c} + \frac{1}{x(b-c)+6c} \]
Hint 2
Reorganize the denominators:
\[ x(b-c)+6c=xb-xc+6c = xb + (\underbrace{6-x}_{=y})c = xb + yc \]
Where \(y=6-\underbrace{x}_{0 \lt x \le 6} \ge 0\) and \(x+y=6\)
Solution
We start by splitting the left-hand side of the inequality into two sums:
\[ \frac{a+1}{x(b-c)+6c}+\frac{b+1}{x(c-a)+6a}+\frac{c+1}{x(a-b)+6b} = \\ = \underbrace{\sum \frac{a}{x(b-c)+6c}}_{S_1} + \underbrace{\sum \frac{1}{x(b-c)+6c}}_{S_2} \]
We observe that we can rewrite the denominator as follows:
\[ x(b-c)+6c=xb-xc+6c = xb + (\underbrace{6-x}_{=y})c = xb + yc \]
where \(y=6-\underbrace{x}_{0 \lt x \le 6} \ge 0\) and \(x+y=6\)
Then, we can express the sums \(S_1\) and \(S_2\) as:
\[ \begin{cases} S_1 = \sum \frac{a}{xb + yc}, \\ S_2 = \sum \frac{1}{xb + yc}. \end{cases} \]
Now, we apply the refinement for \(S_1\):
\[ S_1 \ge \frac{3}{\underbrace{x+y}_{6}} = \frac{1}{2} \]
Next, we apply the Cauchy-Schwarz (CBS) inequality for \(S_2\):
\[ [\frac{1}{xb + yc} + \frac{1}{xc+ya} + \frac{1}{xa+yb}](xb+yc+xc+ya+xa+yb) \overbrace{\ge}^{CBS} \\ \ge (1+1+1)^2 \Leftrightarrow \\ S_2 \ge \frac{9}{(x+y)(a+b+c)} \ge \frac{1}{2} \Leftrightarrow \\ \]
Given that \(S_1 \ge \frac{1}{2}\) and \(S_2 \ge \frac{1}{2}\), we conclude:
\[ S_1 + S_2 \ge 1. \]
Source
Andrei N. Ciobanu
And finally, the next problem is not exactly a refinement, but an interesting “generalisation”:
Let \(a,b,c \) be positive real numbers greater or equal than \(1\), and \(k\in\mathbb{R}_{+}\). Prove that:
\[ \frac{a}{k+b+c}+\frac{b}{k+c+a}+\frac{c}{k+a+b} \ge \frac{3}{k+2} \]
Hint 1
Try applying the Cauchy-Bunyakovsky-Schwarz (CBS) inequality.
Solution
First, apply the CBS inequality:
\[ \Bigl[\frac{a}{k+b+c}+\frac{b}{k+c+a}+\frac{c}{k+a+b}\Bigl] \cdot \] \[ \Bigl[a(k+b+c) + b(k+c+a) + c(k+a+b) \Bigl] \ge (a+b+c)^2 \]
Rearranging, we obtain:
\[ \frac{a}{k+b+c}+\frac{b}{k+c+a}+\frac{c}{k+a+b} \geq \frac{(a+b+c)^2}{k(a+b+c)+2(ab+bc+ca)} \]
Since \(a,b,c \ge 1\), we have \(a + b + c \le ab + bc + ca\). Hence:
\[ \frac{(a+b+c)^2}{k(a+b+c)+2(ab+bc+ca)} \geq \frac{\overbrace{a^2+b^2+c^2}^{\geq ab+bc+ca} + 2(ab+bc+ca)}{(ab+bc+ca)(k+2)} \geq \] \[ \\ \frac{3(ab+bc+ca)}{(k+2)(ab+bc+ca)} = \frac{3}{k+2} \]
The inequality is proven.
When does equality hold?
Titu’s Lemma (Bergstrom)
In 2001, Titu Alexandrescu, who was at that time an USA IMO trainer, gave a lecture on a special case of the Cauchy-Bunyakovsky-Schwartz. Shortly after, one of his results (which was already known in the mathematical world) proved to be extremely effective for solving and “simplifying” difficult inequality questions. The technique was so efficient, that it got the popular name of “Titu’s Lemma”. Titu’s Lemma states:
For any real numbers \(a_1,\dots,a_n\) and any positive real numbers \(b_1,\dots,b_n\) we have:
\[ \frac{a_1^2}{b_1}+\dots+\frac{a_2^2}{b_n}\ge\frac{(a_1+\dots+a_n)^2}{b_1+\dots+b_n} \]
The proof for two terms doesn’t need to involve the CBS inequality and it’s quite straightforward. Why don’t you try it:
Let \(a, b \in \mathbb{R}\) and \(x, y \in \mathbb{R}_{+}\), prove:
\[ \frac{a^2}{x}+\frac{b^2}{y} \ge \frac{(a+b)^2}{x+y} \]
Hint 1
Move everything to the left and simplify the resulting expression:
\[ \frac{a^2}{x}+\frac{b^2}{y}-\frac{(a+b)^2}{x+y} \overbrace{\ge}^{?} 0 \]
Solution
Rewriting the left-hand side:
\[ \frac{a^2}{x}+\frac{b^2}{y}-\frac{(a+b)^2}{x+y} = \frac{a^2y(x+y)+b^2x(x+y)-xy(a^2+b^2+2ab)}{xy(x+y)} = \\ = \frac{(ay-bx)^2}{xy(x+y)} \ge 0 \]
Since the square of a real number is always non-negative, the inequality holds.
Now, let’s try to prove it for 3 terms:
Let \(a, b, c \in \mathbb{R}\) and \(x, y, z \in \mathbb{R}_{+}\). Prove the following inequality:
\[ \frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z}\ge\frac{(a+b+c)^2}{x+y+z} \]
Hint 1
Apply the Cauchy-Schwarz (CBS) inequality for the sequences:
\[ \left(\frac{a}{\sqrt{x}}, \frac{b}{\sqrt{y}}, \frac{c}{\sqrt{z}}\right) \quad \text{and} \quad (\sqrt{x}, \sqrt{y}, \sqrt{z}). \]
Solution
We apply the CBS inequality in the following form:
\[ \left( \frac{a}{\sqrt{x}} \cdot \sqrt{x} + \frac{b}{\sqrt{y}} \cdot \sqrt{y} + \frac{c}{\sqrt{z}} \cdot \sqrt{z} \right)^2 \leq \left( \frac{a^2}{x} + \frac{b^2}{y} + \frac{c^2}{z} \right)(x + y + z). \]
Simplifying the left-hand side:
\[ (a+b+c)^2 \leq \left( \frac{a^2}{x} + \frac{b^2}{y} + \frac{c^2}{z} \right)(x+y+z). \]
Rearranging, we obtain:
\[ \frac{(a+b+c)^2}{x+y+z} \leq \frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z}. \]
This completes the proof.
Any problem that can be solved using the CBS inequality can be solved just as effectively—if not more easily—using Titu’s Lemma.
For \(a \in \mathbb{R}\), prove:
\[ 3(a^4+a^2+1) \ge (a^2+a+1)^2 \]
Solution 1 - CBS
Applying the Cauchy-Schwarz (CBS) inequality in the form:
\[ (1^2+1^2+1^2)(a^4+a^2+1) \ge (1 \cdot a^2 + 1 \cdot a + 1 \cdot 1)^2 \]
Expanding the right-hand side:
\[ 3(a^4+a^2+1) \ge (a^2+a+1)^2. \]
When does equality hold?
Solution 2 - Titu's Lemma
Applying Titu's Lemma (a direct consequence of CBS):
\[ \frac{a^4}{1}+\frac{a^2}{1}+\frac{1}{1} \ge \frac{(a^2+a+1)^2}{3} \]
Multiplying both sides by 3 gives:
\[ 3*(a^4+a^2+1) \ge (a^2+a+1)^2 \]
When does equality hold?
As a cool exercise, try proving Nesbitt’s inequality using Titu’s Lemma:
Let \(a,b,c\) positive real numbers, prove:
\[ \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge\frac{3}{2} \]
Hint 1
Rewrite each term in a form that suggests an application of Titu's Lemma:
\[ \frac{a}{b+c}=\frac{a^2}{a(b+c)} \]
Solution
To align with Titu's Lemma, we rewrite each term on the left-hand side:
\[ \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=\frac{a^2}{a(b+c)}+\frac{b^2}{b(a+c)}+\frac{c^2}{c(a+b)} \]
Applying Titu’s Lemma, we obtain the equivalent inequality:
\[ \frac{a^2}{a(b+c)}+\frac{b^2}{b(a+c)}+\frac{c^2}{c(a+b)} \ge \frac{(a+b+c)^2}{2(ab+bc+ca)} = \\ \frac{a^2+b^2+c^2+2(ab+bc+ca)}{2(ab+bc+ca)} = \\ = 1 + \frac{a^2+b^2+c^2}{2(ab+bc+ca)} \ge \frac{3}{2} \]
We conclude that:
\[ \frac{a^2+b^2+c^2}{2(ab+bc+ca)}\ge\frac{1}{2} \Leftrightarrow a^2 + b^2 + c^2 \ge ab + bc + ca \]
which is a known inequality that completes the proof.
Two of the problems we’ve solved so far become “one-liners” just by applying Titu’s Lemma directly:
Let \(a, b, c\) be positive real numbers, and \(a+b+c=3\). Prove that:
\( \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a} \ge \frac{3}{2} \)
Solution:
Applying Titu's Lemma:
\[ \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a} \ge \frac{(1+1+1)^2}{2(\underbrace{a+b+c}_{=3})} = \frac{3}{2} \]
The equality holds if \(a=b=c=1\).
Let \(a,b,c,x,y,z\) be positive real numbers, and \(x+y+z=a+b+c=1\). Prove that:
\[ \frac{1}{ax+by+cz}+\frac{1}{cx+ay+bz}+\frac{1}{bx+cy+az} \ge 9 \]
Solution:
Applying Titu's Lemma:
\[ \frac{1}{ax+by+cz}+\frac{1}{cx+ay+bz}+\frac{1}{bx+cy+az} \ge \frac{(1+1+1)^2}{(\underbrace{a+b+c}_{=1})(\underbrace{x+y+z}_{=1})} = 9 \]
The equality holds when \(a=b=c=x=y=z=\frac{1}{3}\).
To emphasize the power of Titu’s Lemma, let’s first solve some “harder” inequality problems using traditional methods—relying on tricks and clever manipulations—before demonstrating the much simpler approach with Titu’s Lemma.
Let \(x,y,z\) be positive real numbers. Prove that:
\[ \frac{y^2+z^2}{x}+\frac{z^2+x^2}{y}+\frac{x^2+y^2}{z} \ge 2(x+y+z) \]
Hint 1
To simplify the left-hand side, rewrite each fraction by splitting the numerator:
\[ \frac{y^2+z^2}{x}+\frac{z^2+x^2}{y}+\frac{x^2+y^2}{z} = \frac{y^2}{x}+\frac{z^2}{x}+\frac{x^2}{y}+\frac{z^2}{y}+\frac{x^2}{z}+\frac{y^2}{z} \]
Solution 1 - Clever Tricks
We start by "splitting" the fractions:
\[ \frac{y^2+z^2}{x}+\frac{z^2+x^2}{y}+\frac{x^2+y^2}{z} = \frac{y^2}{x}+\frac{z^2}{x}+\frac{x^2}{y}+\frac{z^2}{y}+\frac{x^2}{z}+\frac{y^2}{z} \]
The next step is to use one of the listed identities:
\[ x^3+y^3=(x+y)(\underbrace{x^2-xy+y^2}_{\ge xy}) \ge (x+y)xy \]
The fact that \(x^2-xy+y^2 \ge xy\) is dirrect consequence of the AM-GM inequality:
\[ x^2+y^2 \overbrace{\ge}^{AM-GM} 2xy \Leftrightarrow x^2 - 2xy + y^2 \ge xy \]
We didivde both sides with \(xy\):
\[ \frac{x^2}{y}+\frac{y^2}{x} \ge x+y \]
In a similar fashion:
\[ \begin{cases} \frac{y^2}{z}+\frac{z^2}{y} \ge y+z \\ \frac{z^2}{x}+\frac{x^2}{z} \ge x+z \end{cases} \]
If we sum-up the three inequalities, the inequality is proven:
\[ \underbrace{\frac{x^2}{y} + \frac{y^2}{x}}_{\ge x+y} + \underbrace{\frac{y^2}{z}+\frac{z^2}{y}}_{\ge z+y} + \underbrace{\frac{z^2}{x}+\frac{x^2}{z}}_{\ge x+z} \ge 2(x+y+z) \]
The equality holds when \(x=y=z\).
Solution 2 - Titu's Lemma
We rewrite the left-hand side:
\[ \frac{y^2+z^2}{x}+\frac{z^2+x^2}{y}+\frac{x^2+y^2}{z} = \frac{y^2}{x}+\frac{z^2}{x}+\frac{x^2}{y}+\frac{z^2}{y}+\frac{x^2}{z}+\frac{y^2}{z} \]
After applying Titu's Lemma:
\[ \frac{y^2}{x}+\frac{z^2}{x}+\frac{x^2}{y}+\frac{z^2}{y}+\frac{x^2}{z}+\frac{y^2}{z} \ge \frac{(y+z+x+z+x+y)^2}{x+x+y+y+z+z} \Leftrightarrow \\ \frac{y^2}{x}+\frac{z^2}{x}+\frac{x^2}{y}+\frac{z^2}{y}+\frac{x^2}{z}+\frac{y^2}{z} \ge \frac{4(x+y+z)^2}{2(x+y+z)} = 2(x+y+z) \]
The equality holds when \(x=y=z\).
Source
RMO 2014, India
Let \(a,b,c,d\) positive real numbers. Prove that:
\[ \frac{a}{b+2c+d} + \frac{b}{c+2d+a} + \frac{c}{d+2a+b} + \frac{d}{a+2b+c} \ge 1 \]
Solution - Clever Tricks
Although it may seem unexpected, this inequality becomes easier to prove by first establishing the following auxiliary inequality:
\[ \frac{u}{x}+\frac{v}{y} \ge \frac{4(uy+vx)}{(x+y)^2}, \quad \forall x,y,u,v \gt 0 \]
To prove this, we use a classical inequality that follows from the AM-GM inequality:
\[ (x+y)^2 \ge 4xy \quad \Leftrightarrow \quad \frac{1}{xy} \ge \frac{4}{(x+y)^2} \]
Now consider the expression:
\[ \frac{u}{x} + \frac{v}{y} = \frac{uy+vx}{xy} \ge \frac{4(ux+uy)}{(x+y)^2} \]
We now apply this inequality by grouping the terms in the original expression:
\[ \begin{cases} \frac{a}{b+2c+d}+\frac{c}{d+2a+b} \ge \frac{2a^2+2c^2+ab+bc+cd+da}{(a+b+c+d)^2} \\ \frac{b}{c+2d+a}+\frac{d}{a+2b+c} \ge \frac{2b^2+2d^2+ab+bc+cd+da}{(a+b+c+d)^2} \end{cases} \]
Adding the two inequalities, we get:
\[ \frac{a}{b+2c+d}+\frac{c}{d+2a+b} + \frac{b}{c+2d+a}+\frac{d}{a+2b+c} \ge \] \[ \ge \frac{2a^2+2c^2+ab+bc+cd+da+2b^2+2d^2+ab+bc+cd+da}{(a+b+c+d)^2} \Leftrightarrow \] \[ \frac{a}{b+2c+d}+\frac{c}{d+2a+b} + \frac{b}{c+2d+a}+\frac{d}{a+2b+c} \ge \] \[ \frac{(a+b+c+d)^2+(a^2+b^2+c^2+d^2-2ac-2bd)}{(a+b+c+d)^2} \Leftrightarrow \] \[ 1+\frac{(a-c)^2+(b-d)^2}{(a+b+c+d)^2} \ge 1 \Leftrightarrow \frac{(a-c)^2+(b-d)^2}{(a+b+c+d)^2} \geq 0 \]
Since squares are always non-negative, the inequality has been proven.
Solution - Titu's Lemma
We begin by rewriting the left-hand side of the inequality to align with the structure required for Titu's Lemma:
\[ \frac{a}{b+2c+d} + \frac{b}{c+2d+a} + \frac{c}{d+2a+b} + \frac{d}{a+2b+c} = \] \[ = \frac{a^2}{a(b+2c+d)}+\frac{b^2}{b(c+2d+a)}+\frac{c^2}{c(d+2a+b)}+\frac{d^2}{d(a+2b+c)} = \] \[ \ge \frac{(a+b+c+d)^2}{2(ab+ad+bc+cd)+4(ac+bd)} \]
To complete the proof, it remains to show that::
\[ a^2+b^2+c^2+d^2 + 2(ab+ad+bc+cd+ac+bd) \ge \] \[ 2(ab+ad+bc+cd) + 4(ac+bd) \Leftrightarrow \] \[ a^2+b^2+c^2+d^2 \ge 2ac+2bd \]
This final inequality is true by the AM-GM inequality (or even directly by Cauchy-Schwarz).
Source
Romanian Math Olympiad, 8th grade, 2005
For the next problems, Titu’s Lemma plays a special role in simplifying them:
Let \(a,b,c\) positive real numbers, such that \(a^2+b^2+c^2=3\). Prove the inequality:
\[ \frac{a}{a+3}+\frac{b}{b+3}+\frac{c}{c+3} \leq \frac{3}{4} \]
Hint 1
For inequalities like this, it's always worth trying "to change the sign" and "create" an equivalent inequality:
\[ \left(1-\frac{a}{a+3}\right)+\left(1-\frac{b}{b+3}\right)+\left(1-\frac{c}{c+3}\right) \geq 3-\frac{3}{4} \]
Solution
We are preparing to use Titu's Lemma, but we first need to change the sign:
\[ \frac{a}{a+3}+\frac{b}{b+3}+\frac{c}{c+3} \leq \frac{3}{4} \Leftrightarrow \] \[ \left(1-\frac{a}{a+3}\right)+\left(1-\frac{b}{b+3}\right)+\left(1-\frac{c}{c+3}\right) \geq 3-\frac{3}{4} \Leftrightarrow \] \[ \frac{3}{3+a}+\frac{3}{3+b}+\frac{3}{3+c} \geq \frac{9}{4} \Leftrightarrow \] \[ \frac{1}{a+3}+\frac{1}{b+3}+\frac{1}{c+3} \geq \frac{3}{4} \]
At this point it's natural to apply Titu's Lemma:
\[ \frac{1}{a+3}+\frac{1}{b+3}+\frac{1}{c+3} \geq \frac{9}{(a+b+c)+9} \tag{1} \]
The last step is to connect the existing condition \(a^2+b^2+c^2=3\) with \(a+b+c\) using the CBS inequality:
\[ (1+1+1)(a^2+b^2+c^2) \geq (a+b+c)^2 \Leftrightarrow 3 \geq a+b+c \tag{2} \]
From (1) and (2), we conclude:
\[ \frac{1}{a+3}+\frac{1}{b+3}+\frac{1}{c+3} \geq \frac{9}{(a+b+c)+9} \geq \frac{9}{12} = \frac{3}{4} \]
Hence, the inequality is proven.
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Arges, 2013
Let \(x,y,z \in (0,1)\) or \(x,y,z \in (1, \infty)\). Prove the following inequality:
\[ \frac{\log_x y}{x+y} + \frac{\log_y z}{y+z} + \frac{\log_z x}{z+x} \geq \frac{9}{2(x+y+z)} \]
Hint 1
Note that:
\[ \prod_{\text{cyc}} \log_x y = 1 \]
Solution
We apply titu's Lemma directly:
\[ \sum_{\text{cyc}} \frac{\log_x y}{x+y} \geq \frac{\left( \sqrt{\log_x y} + \sqrt{\log_y z} + \sqrt{\log_z y}\right)^2}{2(x+y+z)} \]
By applying the AM-GM inequality at the numerator:
\[ \frac{\left( \sqrt{\log_x y} + \sqrt{\log_y z} + \sqrt{\log_z y}\right)^2}{2(x+y+z)} \geq \frac{\left(3\cdot\sqrt{\log_x y \cdot \log_y z \cdot \log_z x}\right)^2}{2(x+y+z)} = \] \[ = \frac{9}{2\cdot(x+y+z)} \]
Equality holds when \(x=y=z\).
Source
Romanian Math Olympiad, Etapa Locala, 10th grade, Arad, 2013
Let \(a,b,c\) positive real numbers such that \(ab+bc+ca=3\). Prove the inequality:
\[ \frac{(a+b)^3}{c} + \frac{(b+c)^3}{a} + \frac{(c+a)^3}{b} \geq 24 \]
Hint 1
Rewrite the left-hand side to prepare it for an application of Titu's Lemma:
\[ \frac{(a+b)^4}{c(a+b)}+\frac{(b+c)^4}{a(b+c)}+\frac{(c+a)^4}{b(c+a)} \]
Solution
We begin by rewriting the original expression in a more convenient form:
\[ \frac{(a+b)^4}{c(a+b)}+\frac{(b+c)^4}{a(b+c)}+\frac{(c+a)^4}{b(c+a)} \ge 24 \]
By applying Titu's Lemma, and then AM-GM for each fraction:
\[ \frac{(a+b)^4}{c(a+b)}+\frac{(b+c)^4}{a(b+c)}+\frac{(c+a)^4}{b(c+a)} \ge \frac{[\overbrace{(a+b)^2}^{\geq 4ab}+\overbrace{(b+c)^2}^{\ge 4bc}+\overbrace{(c+a)^2}^{\ge 4ac}]^2}{2(ab+bc+ca)} \ge \] \[ \ge \frac{[4(ab+bc+ca)]^2}{2(ab+bc+ca)} = \frac{144}{6} = 24 \]
Source
Craciun Gheorghe
Let \(a,b,c\) positive real numbers, prove that:
\[ A = \frac{a^2}{(a+b)(a+c)}+\frac{b^2}{(b+c)(c+a)}+\frac{c^2}{(c+a)(c+b)} \ge \frac{3}{4} \]
Solution
We can dirrectly apply Titu's Lemma:
\[ A \ge \frac{(a+b+c)^2}{(a^2+b^2+c^2)+3(ab+bc+ca)} \Leftrightarrow \\ A \ge \frac{(a+b+c)^2}{(a+b+c)^2 + (ab+bc+ca)} \Leftrightarrow \\ A \ge \frac{1}{1+\frac{ab+bc+ca}{(a+b+c)^2}} \]
At this step, it's enough to prove:
\[ 3(ab+bc+ca) \le (a+b+c)^2 \ \Leftrightarrow \\ a^2+b^2+c^2 \ge ab + bc + ca \]
Equality holds if \(a=b=c=1\).
Source
Crotia Math Olympiad, 2004
Let \(a,b,c\) positive real numbers such that \(a+b+c=1\). Prove the following inequality:
\[ \frac{1}{\sqrt{(a+2b)(b+2a)}} + \frac{1}{\sqrt{(b+2c)(c+2b)}} + \frac{1}{\sqrt{(c+2a)(a+2c)}} \geq 3 \]
Hint 1
Notice that each term \(\sqrt{(a+2b)(b+2a)}\) resembles the geometric mean of two sums. Such expressions often allow a direct comparison with a simpler expression like \(\alpha\,(a+b)\) via the AM-GM inequality.
Solution
We can write \(\sqrt{(a+2b)(b+2a)}\leq\frac{3}{2}(a+b)\). Performing the same step cyclically in \((a,b,c)\) gives:
\[ \sum_{\text{cyc}} \frac{1}{\sqrt{(a+2b)(b+2a)}} \geq \sum_{\text{cyc}} \frac{2}{3(a+b)} \]
Now apply Titu's Lemma:
\[ \sum_{\text{cyc}} \frac{2}{3(a+b)} \geq \frac{2 \cdot (1+1+1)^2}{6(\underbrace{a+b+c}_{=1})} = 3 \]
Hence the original expression is at least 3, establishing the desired inequality. Equality occurs precisely when \(a=b=c=\frac{1}{3}\).
Source
Romanian Math Olympiad, Etapa Locala, 9th grade, Arad, 2013
Let \(a,b,c\) positive real numbers and \(a+b+c=3\), prove that:
\[ \frac{(a+1)^2(b+1)}{2\sqrt{b}(c+a)}+\frac{(b+1)^2(c+1)}{2\sqrt{c}(a+b)}+\frac{(c+1)^2(a+1)}{2\sqrt{a}(b+c)} \ge 6 \]
Hint 1
Can you apply the AM-GM to the denominator to make it more "friendly"?
Hint 2
\[ 2\sqrt{a} \overbrace{\le}^{AM-GM} a+1 \]
Solution
We observe that \(2\sqrt{a} \le a+1, 2\sqrt{b} \le b+1, 2\sqrt{c} \le c+1\):
\[ \sum \frac{(a+1)^2(b+1)}{\underbrace{2\sqrt{b}}_{\le (b+1)}(c+a)} \ge \sum \frac{(a+1)^2(b+1)}{(b+1)(c+a)} = \sum \frac{(a+1)^2}{c+a} \]
In this regard:
\[ \sum \frac{(a+1)^2}{c+a} \overbrace{\ge}^{Titu's} \frac{(a+b+c+3)^2}{2(\underbrace{a+b+c}_{=3})} = 6 \]
The equality holds for \(a=b=c=1\)
Source
Andrei N. Ciobanu
Let \(x_1, x_2, \dots, x_n\) positive real numbers, \(\sum_{i=1}^{n}\frac{1}{x_i}=k\), where is k fixed positive real number, prove that:
\[ \sum_{i=1}^{n}(x_i+\frac{1}{x_i})^2 \ge \frac{(n^2+k^2)^2}{nk^2} \]
Hint 1
We can apply Titu's Lemma in the following manner:
\[ \sum_{i=1}^{n}\frac{(x_i+\frac{1}{x_i})^2}{1} \ge \frac{(\sum_{i=1}^n x_i + \sum_{i=1}^n \frac{1}{x_i})^2}{\underbrace{1+\dots+1}_{n}} \]
Hint 2
Prove:
\[ \sum_{i=1}^nx_i \ge \frac{n^2}{k} \]
Solution
After applying Titu's Lemma:
\[ \sum_{i=1}^{n}\frac{(x_i+\frac{1}{x_i})^2}{1} \ge \frac{(\sum_{i=1}^n x_i + \sum_{i=1}^n \frac{1}{x_i})^2}{\underbrace{1+\dots+1}_{n}} \Leftrightarrow \\ \sum_{i=1}^{n}\frac{(x_i+\frac{1}{x_i})^2}{1} \ge \frac{(\sum_{i=1}^n x_i + k)^2}{n} \Leftrightarrow \\ \sum_{i=1}^{n}\frac{(x_i+\frac{1}{x_i})^2}{1} \ge \frac{(\frac{n^2}{k}+ k)^2}{n} \Leftrightarrow \\ \sum_{i=1}^{n}\frac{(x_i+\frac{1}{x_i})^2}{1} \ge \frac{(n^2+k^2)^2}{nk^2} \]
Equality holds if \(x_1=\dots=x_n=1\) and \(n=k\).
If you are wondering why \(\sum_{i=1}^nx_i \ge \frac{n^2}{k}\), apply the CBS inequality between \((x_1,\dots,x_n)\) and \((\frac{1}{x_1},\dots,\frac{1}{x_n})\).
Source
Andrei N. Ciobanu
Let \(a,b,c\) positive real numbers, prove:
\[ \frac{a^2+1}{b+c}+\frac{b^2+1}{a+c}+\frac{c^2+1}{a+b} \ge 3 \]
Hint 1
Split each term like \(\frac{a^2+1}{b+c}=\frac{a^2}{b+c}+\frac{1}{b+c}\) and apply Titu's Lemma for each group.
Solution
After applying Titu's Lemma:
\[ \frac{a^2+1}{b+c}+\frac{b^2+1}{a+c}+\frac{c^2+1}{a+b} \ge \frac{(a+b+c)^2+9}{2(a+b+c)} \]
So we need to prove:
\[ \frac{(a+b+c)^2+9}{2(a+b+c)} \ge 3 \]
We perform the following substitution: \(a+b+c=x\), then:
\[ x^2-6x+9 \ge 0 \Leftrightarrow (x-3)^3 \ge 0 \]
It's obvious that \((x-3)^2\ge0\).
The equality holds when \(a=b=c=1\).
Source
RMO 2006
Let \(a,b,c \in (0, \infty)\), and \(abc=\frac{1}{3}\). Prove:
\[ \frac{2ab}{a+b}+\frac{2bc}{b+c}+\frac{2ca}{c+a} \ge \frac{a+b+c}{a^3+b^3+c^3} \]
Hint 1
If \(abc=\frac{1}{3}\) then \(ab=\frac{1}{3c}, bc=\frac{1}{3a}, ca=\frac{1}{3b}\). How can we use this?
Hint 2
We have already proven that: \(a^3+b^3 \ge ab(a+b)\).
Solution
We can write:
\[ \frac{2ab}{a+b}+\frac{2bc}{b+c}+\frac{2ca}{c+a} = \frac{2}{3c(a+b)} + \frac{2}{3a(b+c)} + \frac{2}{3b(c+a)} = \\ = \frac{2}{3}[\frac{1}{c(a+b)} + \frac{1}{a(b+c)} + \frac{1}{b(c+a)}] = \\ \frac{2}{3}(\frac{1}{ca+cb}+\frac{1}{ab+ac}+\frac{1}{bc+ba}) \overbrace{\ge}^{\text{Titu's}} \frac{2}{3}*\frac{(1+1+1)^2}{2(ab+bc+ca)} \]
So let's try proving the following:
\[ \frac{3}{ab+bc+ca} \overbrace{\ge}^{?} \frac{a+b+c}{a^3+b^3+c^3} \Leftrightarrow \\ 3(a^3+b^3+c^3) \overbrace{\ge}^{?} (a+b+c)(ab+bc+ca) \]
At this point we will use the following inequalities (note: \(a^3+b^3 \ge ab(a+b)\) was already proven as a previous exercise):
\( \begin{cases} a^3+b^3 \ge ab(a+b) \\ b^3+c^3 \ge bc(b+c) \\ c^3+a^3 \ge ca(c+a) \\ a^3+b^3+c^3 \overbrace{\ge}^{AM-GM} 3abc \end{cases} \)
If we sum-up all inequalities:
\( 3(a^3+b^3+c^3) \ge ab(a+b)+bc(b+c)+ca(c+a)+3abc \Leftrightarrow \\ 3(a^3+b^3+c^3) \ge ab(a+b) + abc + bc(b+c) + abc + ca(c+a) + abc \Leftrightarrow \\ 3(a^3+b^3+c^3) \ge ab(a+b+c)+bc(a+b+c) + ca(a+b+c) \Leftrightarrow \\ 3(a^3+b^3+c^3) \ge (a+b+c)(ab+bc+ca) \)
The equality holds if \(a=b=c\) and \(abc=\frac{1}{3}\)
Let \(a,b,c\) positive real numbers:
\[ \frac{(a^3+1)^2}{b+bc}+\frac{(b^3+1)^2}{c+ca}+\frac{(c^3+1)^2}{a+ba} \ge 3(abc+1) \]
Hint 1
\[a^3+b^3+1\overbrace{\ge}^{AM-GM}3ab\]
Hint 2
\[a^3+1+1 \overbrace{\ge}^{AM-GM} 3a\]
Solution
We apply Titu's Lemma directly:
\[ \sum \frac{(a^3+1)^2}{b+bc} \overbrace{\ge}^{Titu's} \frac{(a^3+b^3+c^3+3)^2}{(a+b+c)+(ab+bc+ca)} \]
Even if not obvious, we can "connect" \(a^3+b^3+c^3+3\) with \(a+b+c+ab+bc+ca\) by applying the AM-GM inequality in the following manner:
\[ \begin{cases} a^3+b^3+1 \ge 3ab \\ b^3+c^3+1 \ge 3bc \\ c^3+a^3+1 \ge 3ca \\ a^3+1+1 \ge 3a \\ b^3+1+1 \ge 3b \\ c^3+1+1 \ge 3c \end{cases} \]
Summing everything up, we obtain \(a^3+b^3+c^3+3 \ge a + b + c + ab+bc+ca\). In this regard:
\[ \sum \frac{(a^3+1)^2}{b+bc} \overbrace{\ge}^{Titu's} \frac{(a^3+b^3+c^3+3)^2}{\underbrace{(a+b+c)+(ab+bc+ca)}_{\le a^3+b^3+c^3+3}} \ge \\ \ge \overbrace{a^3+b^3+c^3}^{\ge3abc}+3 \ge 3abc+3 = 3(abc+1) \]
The equality holds if \(a=b=c=1\).
Source
Andrei N. Ciobanu
Let \(a,b,c\) positive real numbers, \(a+b+c=1\), prove that:
\[ \Bigl(1+\frac{1}{a}\Bigl)\Bigl(1+\frac{1}{b}\Bigl)\Bigl(1+\frac{1}{c}\Bigl) \ge 64 \]
Hint 1
Can you find a lower bound for \(\frac{1}{abc}\)?
Hint 2
Can you prove \(\frac{1}{abc}\ge27\) ?
Solution
Our inequality is equivalent to:
\[ 1+(\underbrace{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}_{S_1})+(\underbrace{\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}}_{S_2})+\underbrace{\frac{1}{abc}}_{S_3} \ge 64 \]
We've formed 3 groups, \(S_1, S_2\) and \(S_3\). We need to found a lower bound for each of them.
Given \(a+b+c=1\), by applying the AM-GM inequality:
\[ \frac{a+b+c}{3}\ge\sqrt[3]{abc} \Leftrightarrow \frac{1}{3} \ge \sqrt[3]{abc} \Rightarrow \frac{1}{abc}\ge\frac{1}{3^3}=\frac{1}{27} \]
So we've found out that \(S_3\ge 27\).
Now, let's work on \(S_1, S_2\):
In the relationship \(a+b+c=1\) if we divide each side by \(abc\):
\[ \frac{1}{bc}+\frac{1}{ca}+\frac{1}{ab}=\frac{1}{abc} \ge 27 \]
This means that \(S_2 \ge 27\).
Lastly, to find the lower bound for \(S_1\) we can apply Titu's Lemma:
\[ \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \ge \frac{(1+1+1)^2}{a+b+c} = 9 \]
We can conclude \(S_1 \ge 9\).
The inequality is proven:
\[ 1+(\underbrace{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}_{S_1 \ge 9})+(\underbrace{\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}}_{S_2 \ge 27})+\underbrace{\frac{1}{abc}}_{S_3 \ge 27} \ge 64 \]
Equality holds if \(a=b=c=\frac{1}{3}\)
Notes: solution was inspired by the solution provided by Alin Pop.
Source
Problem was proposed by Ganciulescu Constantin. Solution inspired by the solution provided by Alin Pop. Problem was posted in the Facebook group "Comunitatea Profesorilor de Matematica".
I have seen this problem under various forms in different books, it's hard to verify the author.
Let \(x,y,z \gt 0\), show that:
\[ \frac{x^3}{z^3+x^2y}+\frac{y^3}{x^3+y^2z}+\frac{z^3}{y^3+z^2x} \ge \frac{3}{2} \]
Hint 1
Simplify things by making the following substitution: \(a=x^3, b=y^3, c=z^3\)
This not exactly the most helpful hint, isn't it?
Well, if you make this substition, we can say that:
\[ \sqrt[3]{a^2b} \overbrace{\le}^{AM-GM} \frac{a+a+b}{3} \]
Solution
To make things simpler , we can do the following substitution: \(a=x^3, b=y^3, c=z^3\):
\[ \frac{a}{c+\sqrt[3]{a^2b}}+\frac{b}{a+\sqrt[3]{b^2c}}+\frac{c}{b+\sqrt[3]{c^2a}} \overbrace{\ge}^{?} \frac{3}{2} \]
Applying AM-GM to the following terms to the denominator:
\[ \begin{cases} \sqrt[3]{a^2b} \le \frac{a+a+b}{3} \\ \sqrt[3]{b^2c} \le \frac{b+b+c}{3} \\ \sqrt[3]{c^2a} \le \frac{c+c+a}{3} \end{cases} \]
Using this we can write:
\[ \frac{a}{c+\sqrt[3]{a^2b}}+\frac{b}{a+\sqrt[3]{b^2c}}+\frac{c}{b+\sqrt[3]{c^2a}} \ge \\ \ge 3[\frac{a}{3c+2a+b}+\frac{b}{3a+2b+c}+\frac{c}{3b+2c+a}] = \\ = 3[\frac{a^2}{3ca+2a^2+ab}+\frac{b^2}{3ab+2b^2+bc}+\frac{c^2}{3bc+2c^2+ca}] \overbrace{\ge}^{Titu's} \\ \ge \frac{3(a+b+c)^2}{2(a^2+b^2+c^2)+4(ab+bc+ca)} = \\ = \frac{3}{2}\frac{(a+b+c)^2}{(a+b+c)^2} = \frac{3}{2} \]
Equality holds for \(a=b=c=x=y=z=1\).
Source
I've lost the source.
More challenges
The problems from this chapter a little more challenging, so don’t get discouraged if won’t be able to solve them after the first try.
Let \(a,b,c \in (0,1)\) and \(x,y,z \in (0, \infty)\) such that:
\[ a^x=bc, \quad b^y=ca, \quad c^z = ab \]
Prove the inequality:
\[ \frac{1}{2+x}+\frac{1}{2+y} + \frac{1}{2+z} \leq \frac{3}{4} \]
Hint 1
Express \(x,y,z\) in terms of logarithms:
\[ x = \log_a bc, \quad y = \log_b ca, \quad z = \log_c ab \\ \]
Hint 2
Change the logarithm base to a common base \(k\):
\[ x = \frac{\log_k b + \log_k c}{\log_k a}, \quad y = \frac{\log_k c + \log_k a}{\log_k b}, \quad z = \frac{\log_k a + \log_k b}{\log_k c} \]
Solution
First, we rewrite \(x,y,z\) using a common logarithm base \(k\):
\[ x = \log_a bc = \frac{\log_k b + \log_k c}{\log_k a} \\ y = \log_b ca = \frac{\log_k c + \log_k a}{\log_k b} \\ z = \log_c ab = \frac{\log_k a + \log_k b}{\log_k c} \\ \]
To simplify notation, introduce:
\[ \alpha=\log_k a, \quad \beta = \log_k b, \quad \gamma = \log_k c \]
Then, we rewrite \(x,y,z\) as:
\[ x = \frac{\beta+\gamma}{\alpha}, \quad y = \frac{\gamma+\alpha}{\beta}, \quad z = \frac{\alpha+\beta}{\gamma} \]
Thus, our inequality transforms into:
\[ \frac{1}{2+\frac{\beta+\gamma}{\alpha}} + \frac{1}{2+\frac{\gamma+\alpha}{\beta}} + \frac{1}{2+\frac{\alpha+\beta}{\gamma}} \le \frac{3}{4} \]
Changing the signs and adding \(3\) to each side:
\[ \left(1-\frac{1}{2+\frac{\beta+\gamma}{\alpha}}\right)+\left(1-\frac{1}{2+\frac{\gamma+\alpha}{\beta}}\right)+\left(1-\frac{1}{2+\frac{\alpha+\beta}{\gamma}}\right) \geq \frac{9}{4} \]
Define \(S=\alpha+\beta+\gamma\):
\[ \left( 1-\frac{\alpha}{S+\alpha} \right)+\left( 1-\frac{\beta}{S+\beta} \right)+\left( 1-\frac{\gamma}{S+\gamma} \right) \ge \frac{9}{4} \]
Applying Titu's Lemma:
\[ S\left( \frac{1}{S+\alpha} + \frac{1}{S+\beta} + \frac{1}{S+\gamma} \right) \ge S*\frac{(1+1+1)^2}{3*S + (\alpha+\beta+\gamma)} = \frac{9S}{4S} = \frac{9}{4} \]
This proves the required inequality.
When does the inequality hold?
Source
Romanian Math Olympiad, 10th grade, 2006
The next problem is an inequality problem “spiced-up” with just a little number theory:
Let \( n \) be a natural number with exactly 12 positive divisors, denoted by:
\[ 0 < x_1 < x_2 < \dots < x_{12} \]
Prove the following inequality:
\[ \frac{x_1 + x_2}{x_3 x_4} + \frac{x_5}{x_6} + \frac{x_8}{x_7} + \frac{x_{11} + x_{12}}{x_9 x_{10}} > \frac{4\sqrt{n}}{n} + 2. \]
Hint 1
We first note that \( x_1 = 1 \) and \( x_{12} = n \), since \( x_1 \) is the smallest and \( x_{12} \) the largest positive divisor of \( n \).
Hint 2
For all \( i = 1, 2, \dots, 12 \), it holds that:
\[ x_i \cdot x_{13 - i} = n. \]
Solution
We first note that \( x_1 = 1 \) and \( x_{12} = n \), since \( x_1 \) is the smallest and \( x_{12} \) the largest positive divisor of \( n \).
Also, for all \( i = 1, 2, \dots, 12 \), it holds that:
\[ x_i \cdot x_{13 - i} = n. \]
Applying the Arithmetic Mean–Geometric Mean (AM–GM) inequality to the first and last terms yields:
\[ \frac{x_1 + x_2}{x_3 x_4} + \frac{x_{11} + x_{12}}{x_9 x_{10}} > 2\sqrt{\frac{(x_1 + x_2)(x_{11} + x_{12})}{x_3 x_4 x_9 x_{10}}}. \]
Since \( x_3 x_4 \cdot x_9 x_{10} = n^2 \), and using the divisor symmetry:
\[ > 2\sqrt{\frac{(x_1 + x_2)(x_{11} + x_{12})}{n^2}}. \]
Now apply Cauchy-Schwarz or use the fact that \( x_1 = 1 \), \( x_{12} = n \), and the symmetry suggests \( x_2 \cdot x_{11} = n \Rightarrow x_2 = \frac{n}{x_{11}} \). This motivates bounding the sum \( x_1 + x_2 \) and \( x_{11} + x_{12} \) in terms of \( \sqrt{n} \). Using that:
\[ (x_1 + x_2)(x_{11} + x_{12}) \geq (\sqrt{n} + \sqrt{n})^2 = 4n, \]
We get:
\[ 2\sqrt{\frac{(x_1 + x_2)(x_{11} + x_{12})}{n^2}} > 2\sqrt{\frac{4n}{n^2}} = \frac{4\sqrt{n}}{n}. \]
For the remaining two terms:
\[ \frac{x_5}{x_6} + \frac{x_8}{x_7} \geq 2\sqrt{\frac{x_5 x_8}{x_6 x_7}} = 2\sqrt{\frac{x_5 x_8}{x_6 x_7}} = 2. \]
Thus, the full expression satisfies:
\[ \frac{x_1 + x_2}{x_3 x_4} + \frac{x_5}{x_6} + \frac{x_8}{x_7} + \frac{x_{11} + x_{12}}{x_9 x_{10}} > \frac{4\sqrt{n}}{n} + 2. \]
Now, can you prove the strict nature of the inequality ?
Source
Andrei N. Ciobanu
In a similar fashion:
Prove that for any integer \(n \gt 1 \) the sum \(S\) of all divisors of \(n\) satisfies the following inequality:
\[ k\cdot\sqrt{n} < S \]
Where \(k\) is the number of divisors of \(n\).
Hint 1
Let the divisors of \(n\) be arranged in increasing order:
\[ 1 = d_1 < d_2 < \dots < d_k = n \]
Observe that for each \(i = 1, 2, \dots, k\), we have:
\[ n = d_k \cdot d_{k+1-i} \]
Solution
Let the divisors of \(n\) be:
\[ 1 = d_1 < d_2 < \dots < d_k = n \]
Then for each \(i = 1, 2, \dots, k\), it holds that:
\[ n = d_k \cdot d_{k+1-i} \tag{1} \]
The sum \(S\) of all divisors of \(n\) is given by:
\[ S=\sum_{i=1}^k d_i = d_1 + d_2 + \dots + d_k \]
To apply the AM-GM inequality, consider pairing the divisors symmetrically:
\[ S = \frac{2}{2} \cdot (d_1+ \dots + d_k) = \frac{1}{2} \cdot \sum^k_{i=1}(d_i + d_{k-i+1}) \overbrace{>}^{\text{AM-GM}} \sum_{i=1}^k \sqrt{d_i \cdot d_{k-i+1}} = \] \[ = \underbrace{\sqrt{n}+\sqrt{n}+\dots+\sqrt{n}}_{\text{k times}} = k\cdot\sqrt{n} \tag{2} \]
This proves our inequality.
Source
Belarus, 1999
Let \(a,b,c \in \mathbb{R}^{*}_{+}\) such that \(a+b+c=1\). Prove the inequality:
\[ (ab)^{\frac{5}{4}} + (bc)^{\frac{5}{4}} + (ca)^{\frac{5}{4}} \lt \frac{1}{4} \]
Hint 1
Try applying the Cauchy–Schwarz inequality to terms of the form \((ab)^{5/4}\)
Solution
To get rid of the exponents we apply the CBS inequality in the following manner:
\[ \left[(ab)^{\frac{5}{4}} + (bc)^{\frac{5}{4}}) + (ca)^{\frac{5}{4}} \right]^2 \leq (\sqrt{ab}+\sqrt{bc}+\sqrt{ca})\left[ (ab)^2 + (bc)^2 + (ca)^2 \right] \tag{1} \]
The first term from the right hand side is \(\leq 1\), something that can be easily proved using the AM-GM inequality:
\[ \sqrt{ab}+\sqrt{bc}+\sqrt{ca} \leq \frac{a+b}{2} + \frac{b+c}{2} + \frac{c+a}{2} = 1 \tag{2} \]
It remains to prove that:
\[ \sqrt{(ab)^2 + (bc)^2 + (ca)^2} \lt \frac{1}{4} \Leftrightarrow \] \[ \Leftrightarrow (ab)^2 + (bc)^2 + (ca)^2 \lt \frac{1}{16} \]
Without loss of generality we can assume \(a \geq b \geq c\). From the AM-GM inequality we know that:
\[ \frac{a+(b+c)}{2} \geq \sqrt{a(b+c)} \Leftrightarrow \] \[ \frac{1}{2} \geq \sqrt{a(b+c)} \Leftrightarrow \] \[ \frac{1}{16} \geq a^2(b+c)^2 = a^2(b^2+2bc+c^2) \Leftrightarrow \] \[ \frac{1}{16} \geq a^2b^2+a^2c^2+2 \cdot a^2\cdot bc \gt a^2b^2 + c^2a^2 + b^2c^2 \tag{3} \]
Multiplying \((2)\) and \((3)\) proves the required inequality.
Source
Romanian Math Olympiad, National Phase, Shortlist, 2003, Dinu Teodorescu
In Part 2
This article was just an introduction. In the upcoming articles in this series, I plan to discuss the following topics: Jensen’s Inequality, Hölder’s Inequality, Radon’s Inequality, Chebyshev’s Inequality, Bernoulli’s Inequality, the PQR Technique, Calculus Techniques, and Lagrange Multipliers.
Where to go next ?
If you have started to develop a taste for solving inequality problems, there are several excellent resources that can help you advance further.
First of all, if you want to read a more “serious” material, I recommend you to go through Vasile Cartoaje’s books:
- Mathematical Inequalities, Volume 1, Symmetrical Polynomial Inequalities
- Mathematical Inequalities, Volume 2, Symmetric Rational and Nonrational Inequalities
- Mathematical Inequalities, Volume 3, Cyclic and Noncyclic Inequalities, Vasile Cirtoaje
- Mathematical Inequalities, Volume 4, Extensions and Refinements of Jensen’s Inequality, Vasile Cirtoaje
- Mathematical Inequalities, Volume 5, Other Recent Methods For Creating and Solving Inequalities, Vasile Cirtoaje, they are amazing.
Secondly there are multiple articles online with similar content (most of them are accesible as a PDF files). For example:
- Basics Of Olympiad Inequalities, Samin Riasat
- Eeshan Banerjee, Titu’s Lemma
- Introduction to Olympiad Inequalities, Sanja Simonovikj
- Titu’s Lemma, Pankaj Agarwal
I recommend you also the following Facebook groups where people gather to actually solve “difficult inequalities” (and not only):
CutTheKnot has a quite a few gems with full solutions available.
Leo Giugiuc’s Blog (who’s one of our “local experts” in inequalities) blog contains some advanced inequalities that are not easily solvable using conventional techniques.
]]>